Introducción

Una gráfica o una representación gráfica o un gráfico, es un tipo de representación de datos, generalmente cuantitativos, mediante recursos visuales (líneas, vectores, superficies o símbolos), para que se manifieste visualmente la relación matemática o correlación estadística que guardan entre sí.

Wikipedia

Paquetes de R para gráficos

R posee una serie de paquetes construido para la visualización de datos que hacen que tengan una excelente presentación. Empezando por funciones del núcleo base, hasta paquetes que elaboran gráficos interactivos

Elegir el gráfico adecuado es muy importante pues existen diferentes alternativos y se debe escoger el apropiado para representar los datos. El tipo de dato determina el tipo de grafico asi:

Tipo de variable	Escala	Gráfico
Cualitativas
	Nominal	torta
	Ordinal	barras

Cuantitativas	Intervalo-razón	diagrama de tallos y hojas
		histograma
		diagrama de cajas
		diagrama de densidad
		diagrama de puntos
		diagrama de lineas
		diagrama de radar
		gráfico likert
		mapa de calor

Gráficos variables cualitativas con R base

Gráfico de tortas

a=rep("Cultutal", 360145)
b=rep("Pastoral", 61496)
c=rep("Bienestar",49912)
d=rep("Deportivo",11777)
data=c(a,b,c,d)
t=table(data)
lbs=c("Cultural", "Pastoral", "Bienestar", "Deportivo")
pct=round(t/sum(t)*100)
labs=paste(lbs, pct)
labs=paste(labs, "%", sep = " ") 
pie(t, labels=labs, main=" Participación eventos Medio Universitario",
    col = paleta4)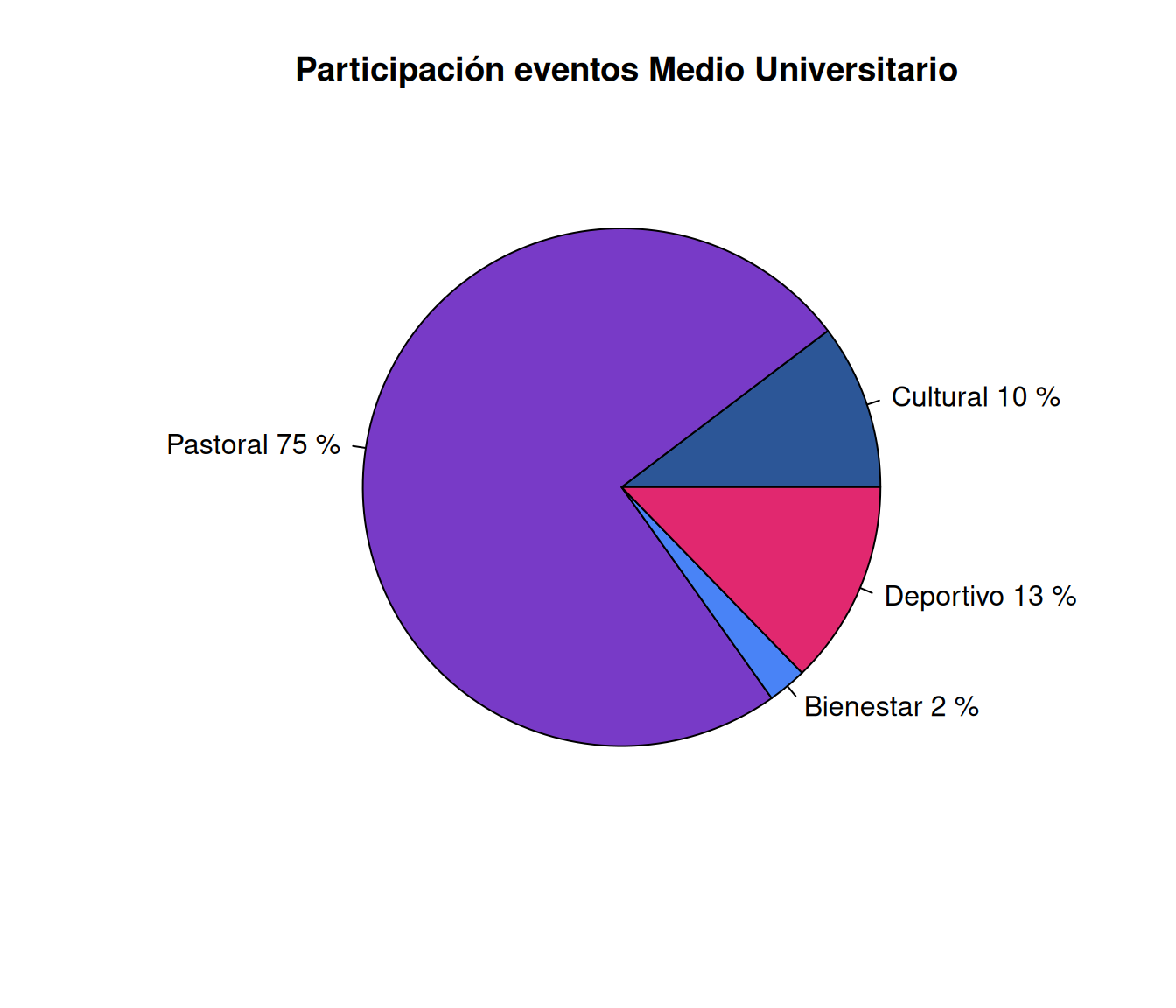

Diagrama de barras

ev=c(4,  8, 12, 43, 32)
names(ev)=c("Muy regular", "Regular", "Bueno", "Muy bueno","Excelente")
barplot(ev, col=c("#ff5b00","#dcf600","#7dbd00","#659cef","#2956b2"), main = "Evaluación proceso de inducción")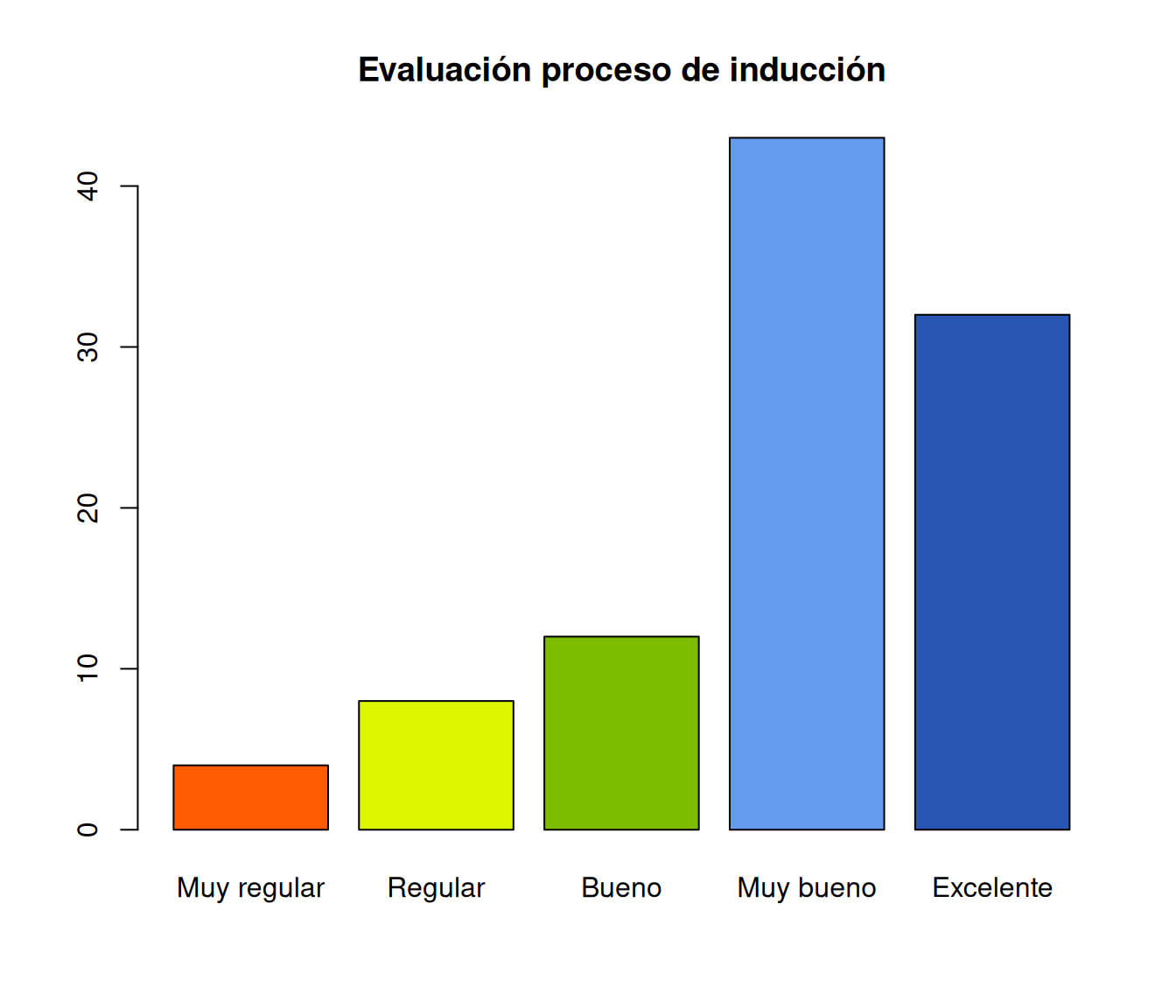

Diagrama de barras dos variables

counts <- table(mtcars$vs, mtcars$gear); rownames(counts)=c("Montor en linea", "Motor en V")
barplot(counts, main="Numero de cambios adelante por Tipo de motor",  xlab="Numero de cambios adelante ",col=c(c6,c2),
  legend = rownames(counts))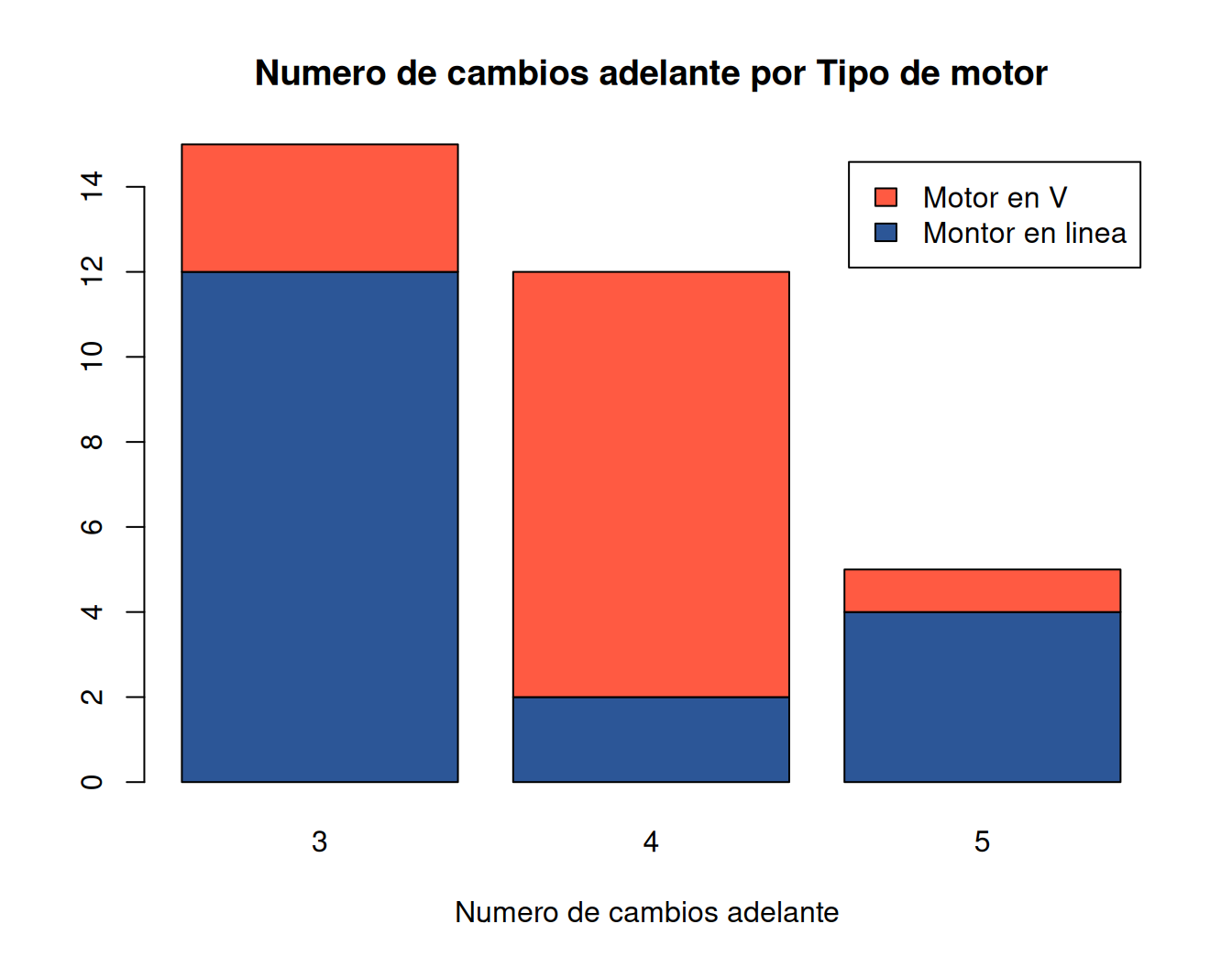

Gráficas variables cuantitativas con R base

Diagrama de árbol

nf=c(4.1, 2.7, 3.1, 3.2, 3.0, 3.2, 2.0, 2.4, 1.6, 3.2, 3.1, 2.6, 2.0, 2.4, 2.8, 3.3, 4.0, 3.4, 3.0, 3.1, 2.7, 2.7, 3.0, 3.8, 3.2, 2.2, 3.5, 3.5, 3.8, 3.5, 3.9, 4.2, 4.3, 3.9, 3.2, 3.5, 3.5, 3.7, 4.1, 3.7, 3.5, 3.6, 3.2, 3.1, 3.4, 3.0, 3.0, 3.0, 2.7, 1.7, 3.6, 2.1, 2.4, 3.0, 3.1, 2.5, 2.5, 3.6, 2.2, 2.4, 3.1, 3.3, 2.7, 3.7, 3.0, 2.7, 3.0, 3.2, 3.1, 2.4, 3.0, 2.7, 2.5, 3.0, 3.0, 3.0, 3.2, 3.1, 3.8, 4.1, 3.7, 3.5, 3.0, 3.7, 3.7, 4.1, 3.7, 3.9, 3.7, 2.0)
stem(nf)


  The decimal point is at the |

  1 | 67
  2 | 00012244444
  2 | 555677777778
  3 | 0000000000000011111111222222223344
  3 | 555555566677777777888999
  4 | 0111123

Este diagrama ordena los datos de manera que se puede determinar tanto en mínimo (1.6) como el máximo (4.3) , además de visualizar donde están la mayor concentración de ellos.

Histograma

nf=c(4.1, 2.7, 3.1, 3.2, 3.0, 3.2, 2.0, 2.4, 1.6, 3.2, 3.1, 2.6, 2.0, 2.4, 2.8, 3.3, 4.0, 3.4, 3.0, 3.1, 2.7, 2.7, 3.0, 3.8, 3.2, 2.2, 3.5, 3.5, 3.8, 3.5, 3.9, 4.2, 4.3, 3.9, 3.2, 3.5, 3.5, 3.7, 4.1, 3.7, 3.5, 3.6, 3.2, 3.1, 3.4, 3.0, 3.0, 3.0, 2.7, 1.7, 3.6, 2.1, 2.4, 3.0, 3.1, 2.5, 2.5, 3.6, 2.2, 2.4, 3.1, 3.3, 2.7, 3.7, 3.0, 2.7, 3.0, 3.2, 3.1, 2.4, 3.0, 2.7, 2.5, 3.0, 3.0, 3.0, 3.2, 3.1, 3.8, 4.1, 3.7, 3.5, 3.0, 3.7, 3.7, 4.1, 3.7, 3.9, 3.7, 2.0)

h1 = hist(nf, main = "Nota final matemáticas fundamentales", xlab = "nota", ylab="frecuencias absolutas", labels=TRUE, col=c6, ylim = c(0,30))
abline(v=3,col="#f6b915", lwd=2)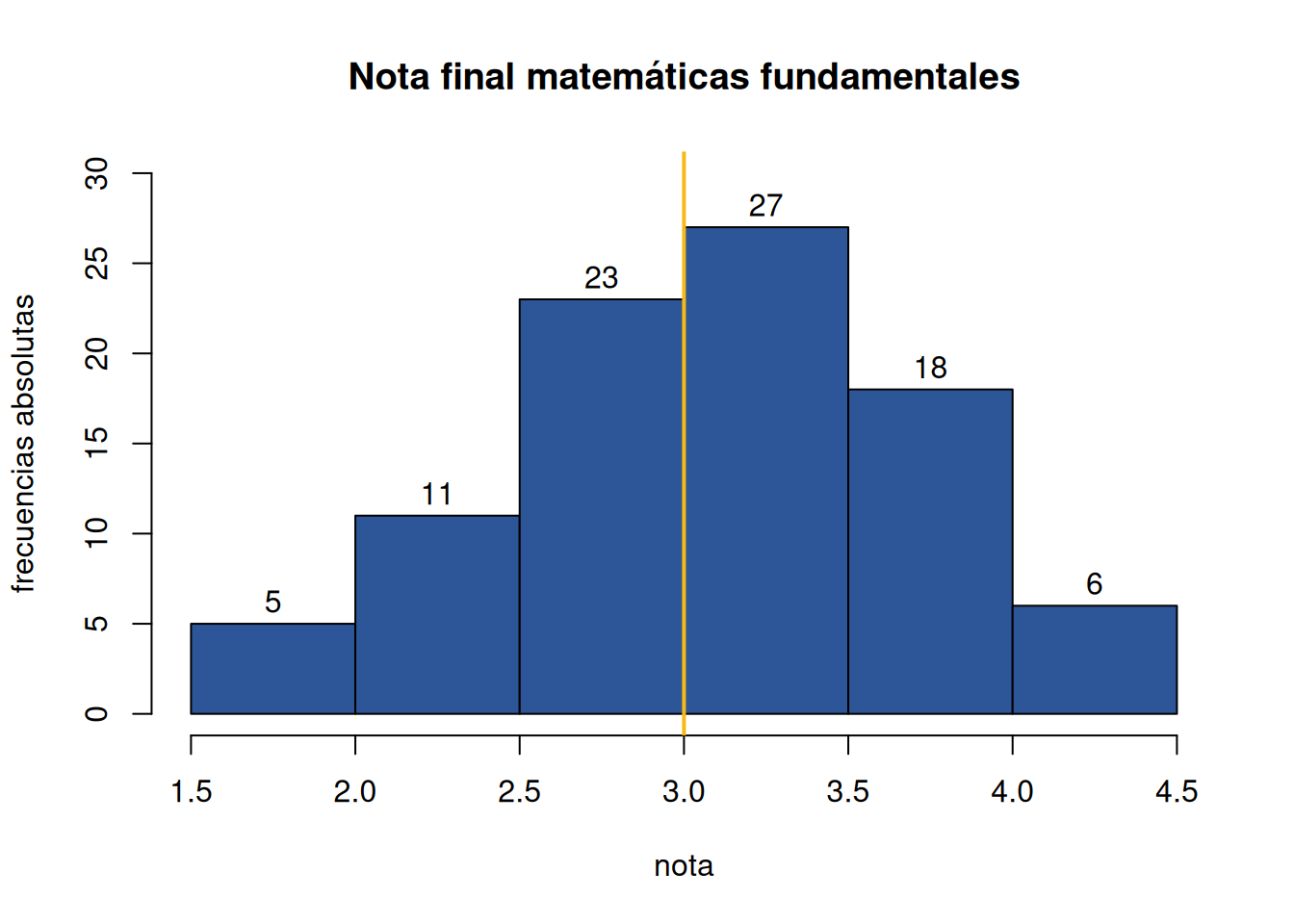

h1

$breaks
[1] 1.5 2.0 2.5 3.0 3.5 4.0 4.5

$counts
[1]  5 11 23 27 18  6

$density
[1] 0.1111111 0.2444444 0.5111111 0.6000000 0.4000000 0.1333333

$mids
[1] 1.75 2.25 2.75 3.25 3.75 4.25

$xname
[1] "nf"

$equidist
[1] TRUE

attr(,"class")
[1] "histogram"

Diagrama de densidad

nf=c(4.1, 2.7, 3.1, 3.2, 3.0, 3.2, 2.0, 2.4, 1.6, 3.2, 3.1, 2.6, 2.0, 2.4, 2.8, 3.3, 4.0, 3.4, 3.0, 3.1, 2.7, 2.7, 3.0, 3.8, 3.2, 2.2, 3.5, 3.5, 3.8, 3.5, 3.9, 4.2, 4.3, 3.9, 3.2, 3.5, 3.5, 3.7, 4.1, 3.7, 3.5, 3.6, 3.2, 3.1, 3.4, 3.0, 3.0, 3.0, 2.7, 1.7, 3.6, 2.1, 2.4, 3.0, 3.1, 2.5, 2.5, 3.6, 2.2, 2.4, 3.1, 3.3, 2.7, 3.7, 3.0, 2.7, 3.0, 3.2, 3.1, 2.4, 3.0, 2.7, 2.5, 3.0, 3.0, 3.0, 3.2, 3.1, 3.8, 4.1, 3.7, 3.5, 3.0, 3.7, 3.7, 4.1, 3.7, 3.9, 3.7, 2.0)
plot(density(nf), main="Distribucion de las notas de matematias fundamentales", col=c6, lwd=2)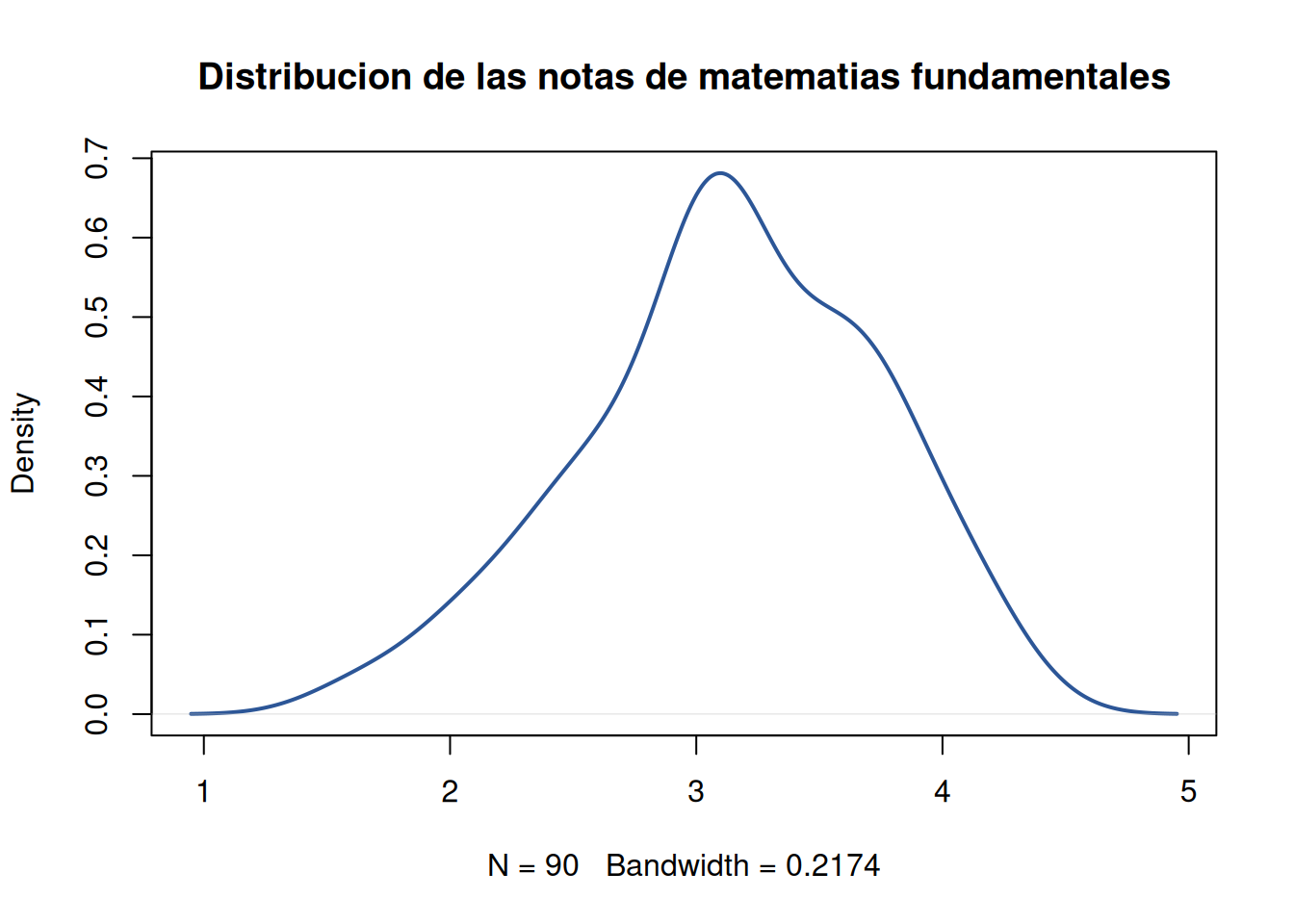

Diagrama de cajas

nf=c(4.1, 2.7, 3.1, 3.2, 3.0, 3.2, 2.0, 2.4, 1.6, 3.2, 3.1, 2.6, 2.0, 2.4, 2.8, 3.3, 4.0, 3.4, 3.0, 3.1, 2.7, 2.7, 3.0, 3.8, 3.2, 2.2, 3.5, 3.5, 3.8, 3.5, 3.9, 4.2, 4.3, 3.9, 3.2, 3.5, 3.5, 3.7, 4.1, 3.7, 3.5, 3.6, 3.2, 3.1, 3.4, 3.0, 3.0, 3.0, 2.7, 1.7, 3.6, 2.1, 2.4, 3.0, 3.1, 2.5, 2.5, 3.6, 2.2, 2.4, 3.1, 3.3, 2.7, 3.7, 3.0, 2.7, 3.0, 3.2, 3.1, 2.4, 3.0, 2.7, 2.5, 3.0, 3.0, 3.0, 3.2, 3.1, 3.8, 4.1, 3.7, 3.5, 3.0, 3.7, 3.7, 4.1, 3.7, 3.9, 3.7, 2.0)
boxplot(nf, main="Nota final matemáticas fundamentales",col=c4, las=1)
abline(h=3, col="red")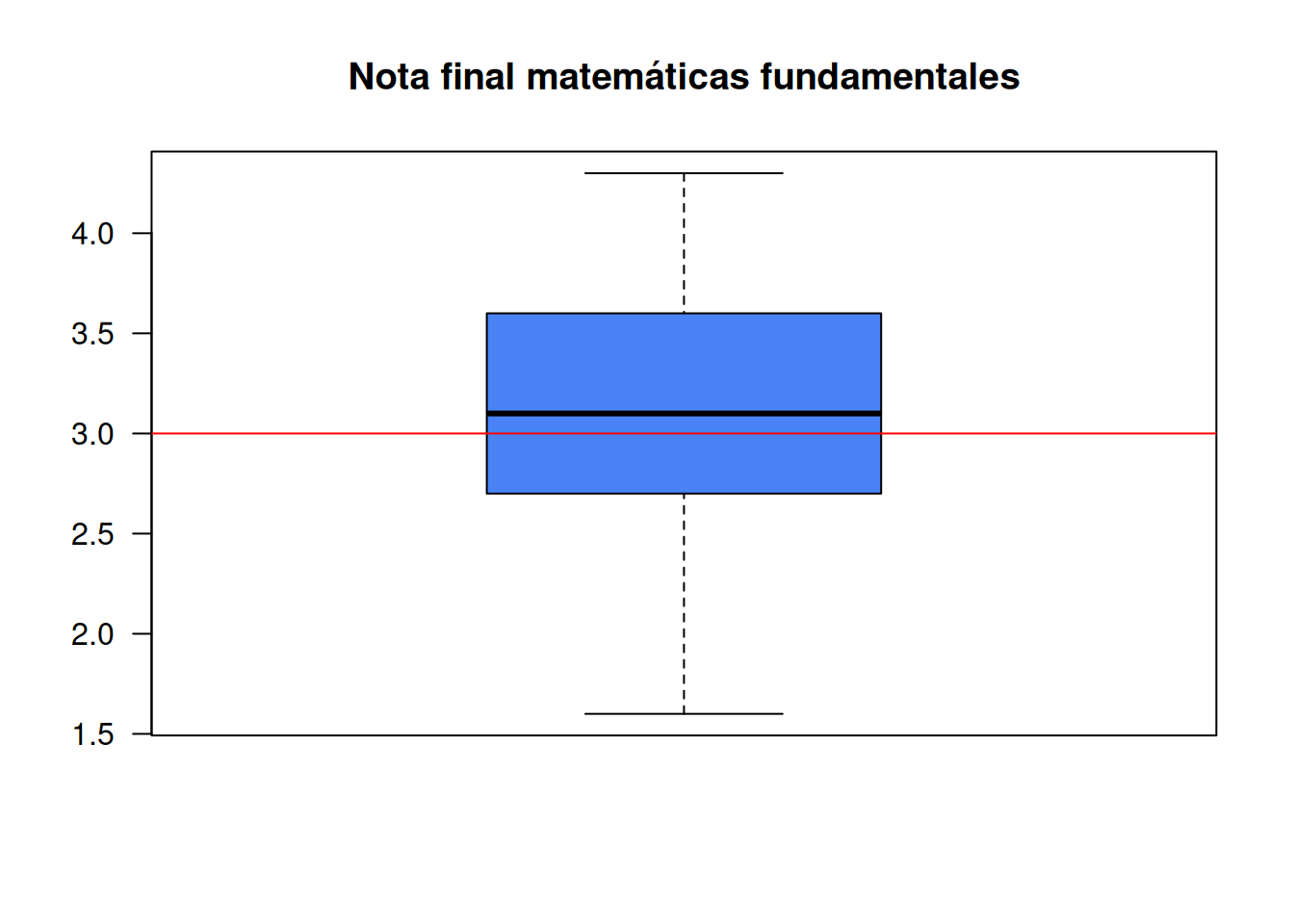

Diagrama de cajas

nf=c(4.1, 2.7, 3.1, 3.2, 3.0, 3.2, 2.0, 2.4, 1.6, 3.2, 3.1, 2.6, 2.0, 2.4, 2.8, 3.3, 4.0, 3.4, 3.0, 3.1, 2.7, 2.7, 3.0, 3.8, 3.2, 2.2, 3.5, 3.5, 3.8, 3.5, 3.9, 4.2, 4.3, 3.9, 3.2, 3.5, 3.5, 3.7, 4.1, 3.7, 3.5, 3.6, 3.2, 3.1, 3.4, 3.0, 3.0, 3.0, 2.7, 1.7, 3.6, 2.1, 2.4, 3.0, 3.1, 2.5, 2.5, 3.6, 2.2, 2.4, 3.1, 3.3, 2.7, 3.7, 3.0, 2.7, 3.0, 3.2, 3.1, 2.4, 3.0, 2.7, 2.5, 3.0, 3.0, 3.0, 3.2, 3.1, 3.8, 4.1, 3.7, 3.5, 3.0, 3.7, 3.7, 4.1, 3.7, 3.9, 3.7, 2.0)
cc=c(20, 10, 20, 20, 20, 20, 20, 20, 20, 30, 20, 20, 20, 10, 30, 20, 20, 30, 20, 30, 30, 20, 10, 30, 20, 20, 30, 30, 10, 20, 10, 20, 20, 20, 10, 20, 10, 20, 20, 30, 30, 30, 10, 30, 20, 20, 20, 20, 20, 20, 10, 20, 30, 30, 10, 10, 10, 20, 10, 20, 10, 30, 20, 10, 20, 30, 10, 30, 30, 30, 20, 30, 30, 30, 30, 30, 30, 20, 10, 30, 10, 20, 20, 10, 20, 20, 20, 20, 10, 20)
labs=c("Ing. de Sistemas","Ing. Industrial","Ing. Mecánica")
boxplot((nf~cc),main="Nota final matemáticas fundamentales por carrera", 
        col=c(c4,c5,c6), names=labs, xlab = "carrera", ylab = "nota")
abline(h=3, col=c2,  lwd=2)
abline(h=4, col=c3, lwd=2)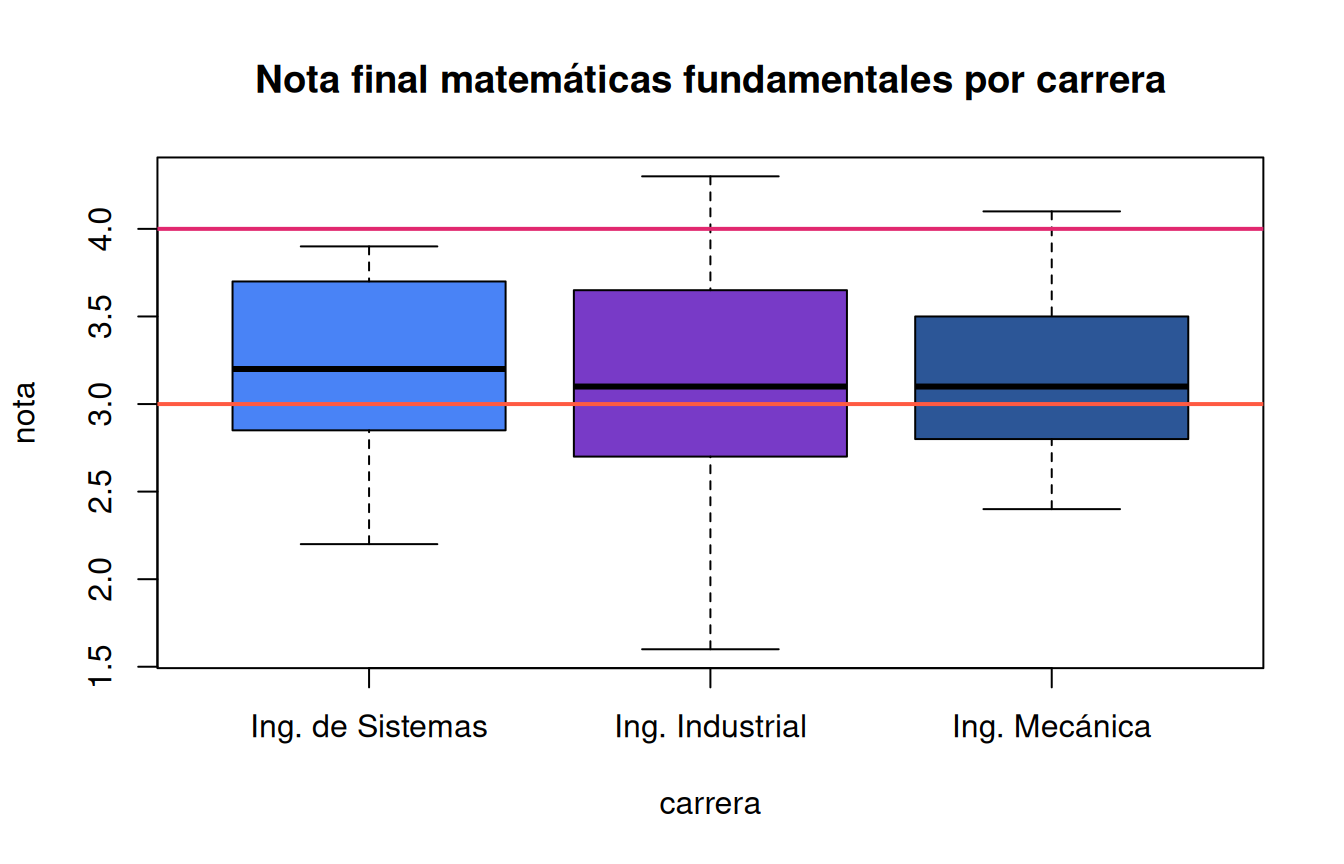

Diagrama de dispersión

ed=round(rnorm(90,18,1),1)
plot(ed,nf, main="Edad vs Nota final matemáticas fundamentales", ylim = c(0,5), xlab = "Edad", ylab = "Nota final",col="#447270",pch=19)
grid()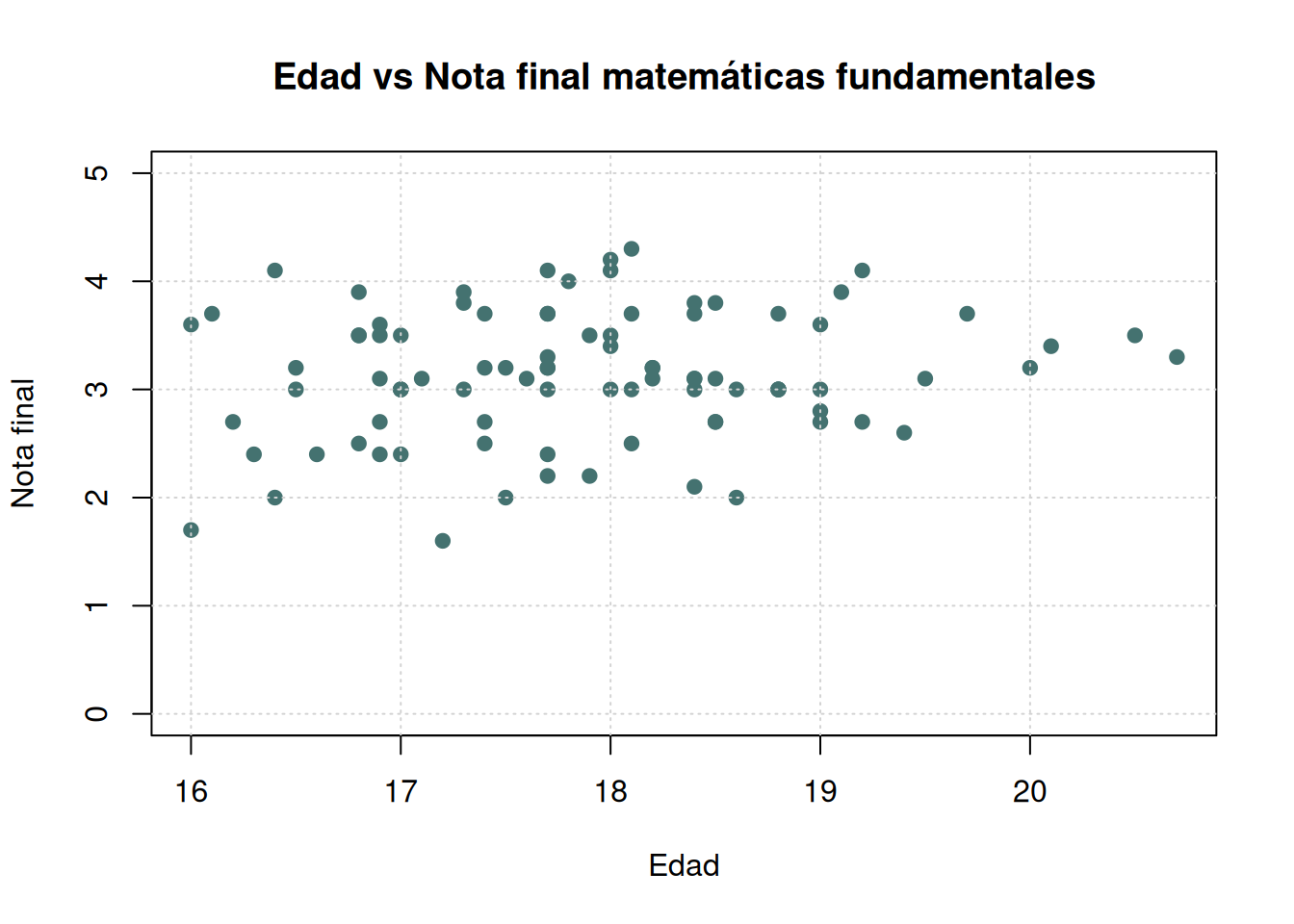

Gráfica de series de tiempo

plot(AirPassengers, main="Numero de pasajeros por mes", col=c6, lwd = 2)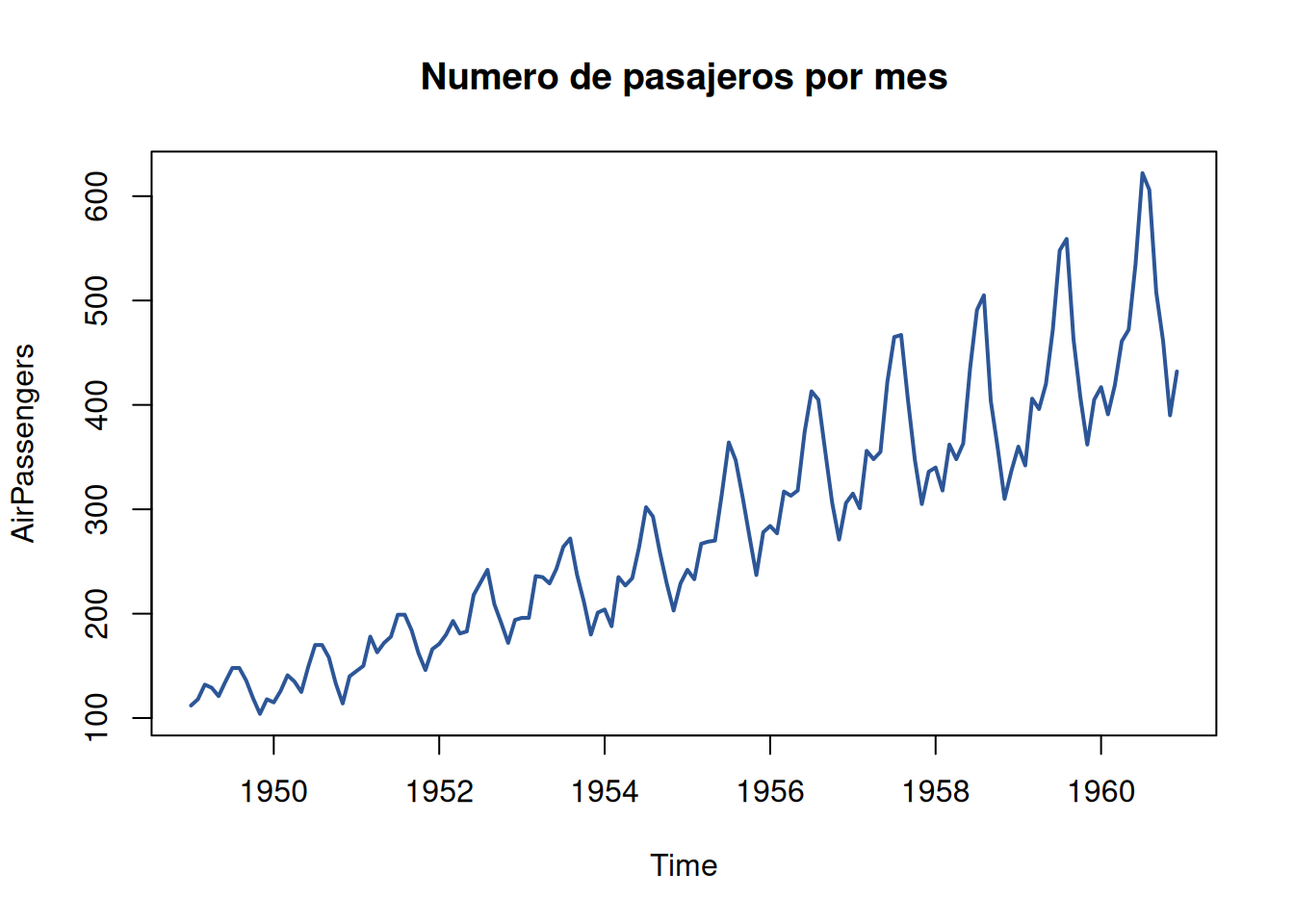

Resumen

x=rnorm(100,100,20)
y=rnorm(100,100,25)
z=rbinom(100,4,0.30)
t=1:100
par(mfrow=c(2, 2))
pie(table(z))
barplot(table(z))
stem(x)


  The decimal point is 1 digit(s) to the right of the |

   5 | 4
   6 | 269
   7 | 123459
   8 | 011233444555567889
   9 | 00001225566667777888899
  10 | 0345556666899
  11 | 000113445567888
  12 | 0012223333445678
  13 | 002
  14 | 0
  15 | 0

hist(x)
boxplot(x)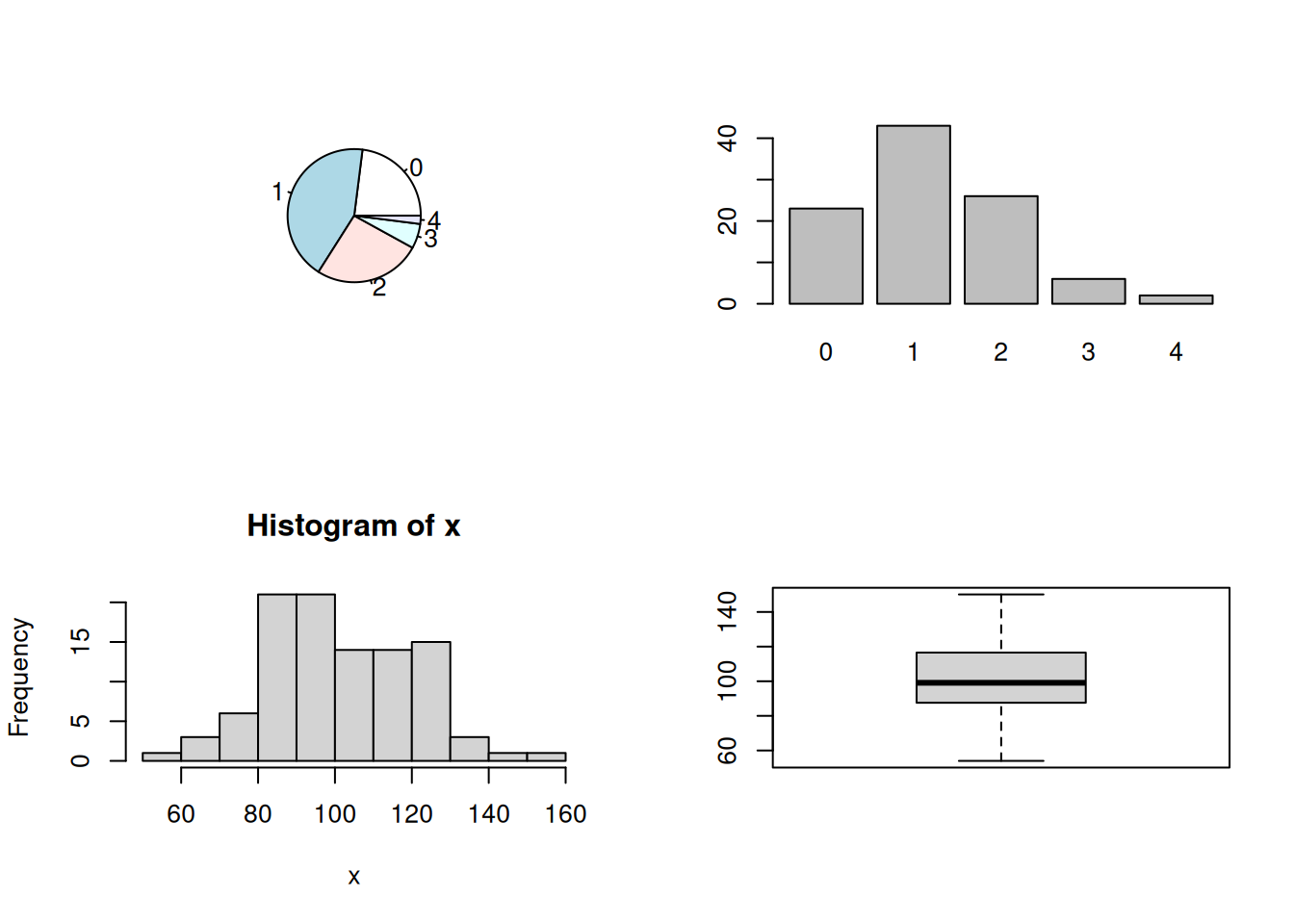

plot(x,y)
plot(t,y, type="l")
plot(density(x))
par(mfrow=c(1, 1))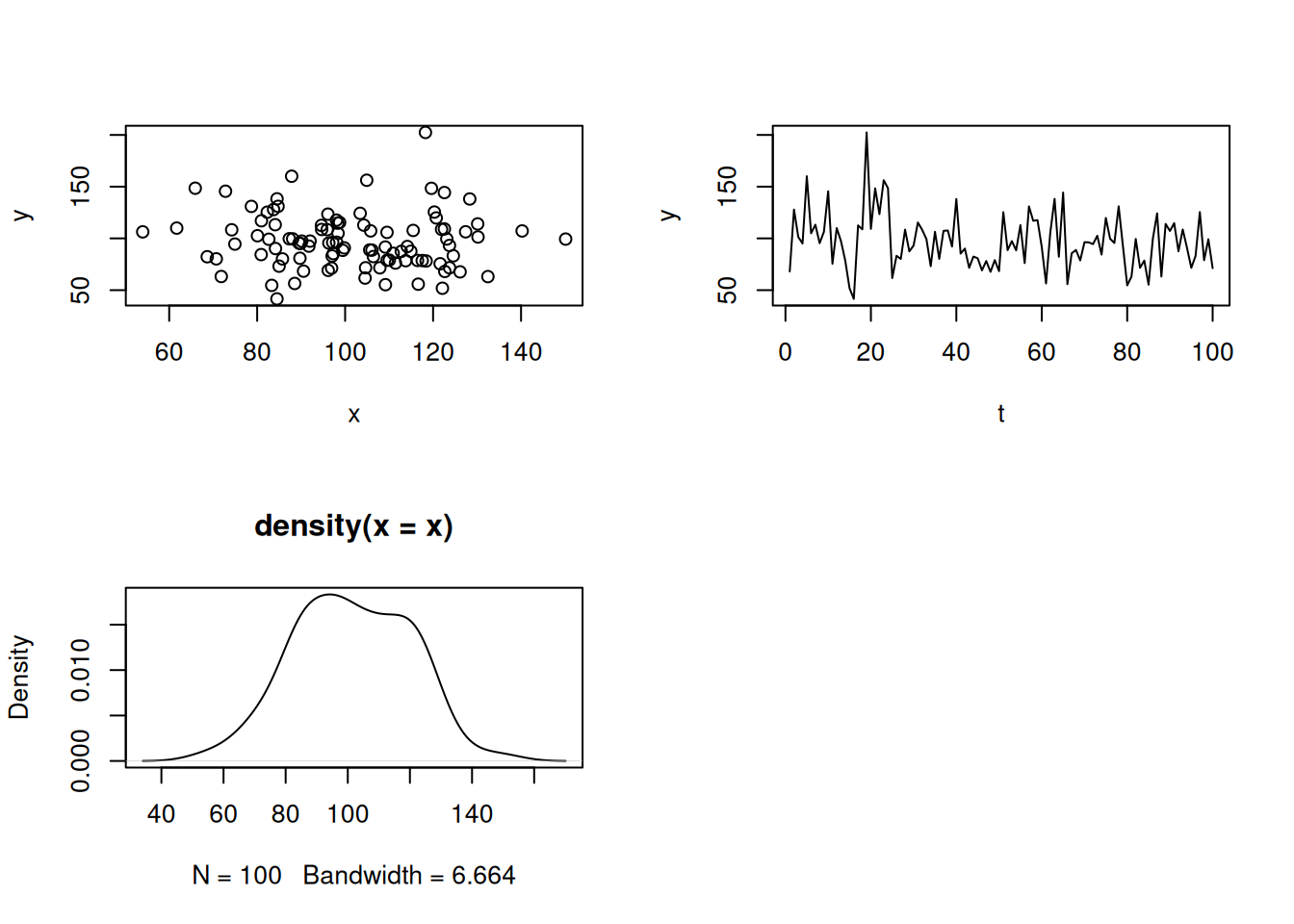

Gráficos con ggplot2

Data: capa de los datos
Aesthetics: capa estética (aes), definimos las variables a utilizar en el gráfico
Geometries: capa de geometrías, se define el tipo de gráfica a realizar
Facets: capa de facetas, permite detallar la gráfica por categorías
Statistics: capa de estadística, permite agregar modelos
Coordinates: capa de coordenadas, permite ajustar las escalas de los ejes
Theme: capas de características del gráfico que no dependen de los datos

Primer paso: Instalar y cargar la libreria

# Instalar ggplot2 si no lo tienes
install.packages("ggplot2")

# Cargar la librería ggplot2
library(ggplot2)

# Instalar ggplot2 si no lo tienes
install.packages("ggplot2")

# Cargar la librería ggplot2
library(ggplot2)

Segundo paso : Declarar la base de datos y las varibles

p <- ggplot(mtcars, aes(x = wt, y = mpg))
p

Cuarto paso : Crear grafico base con las diferentes geometrías

p <- p + geom_point()  
p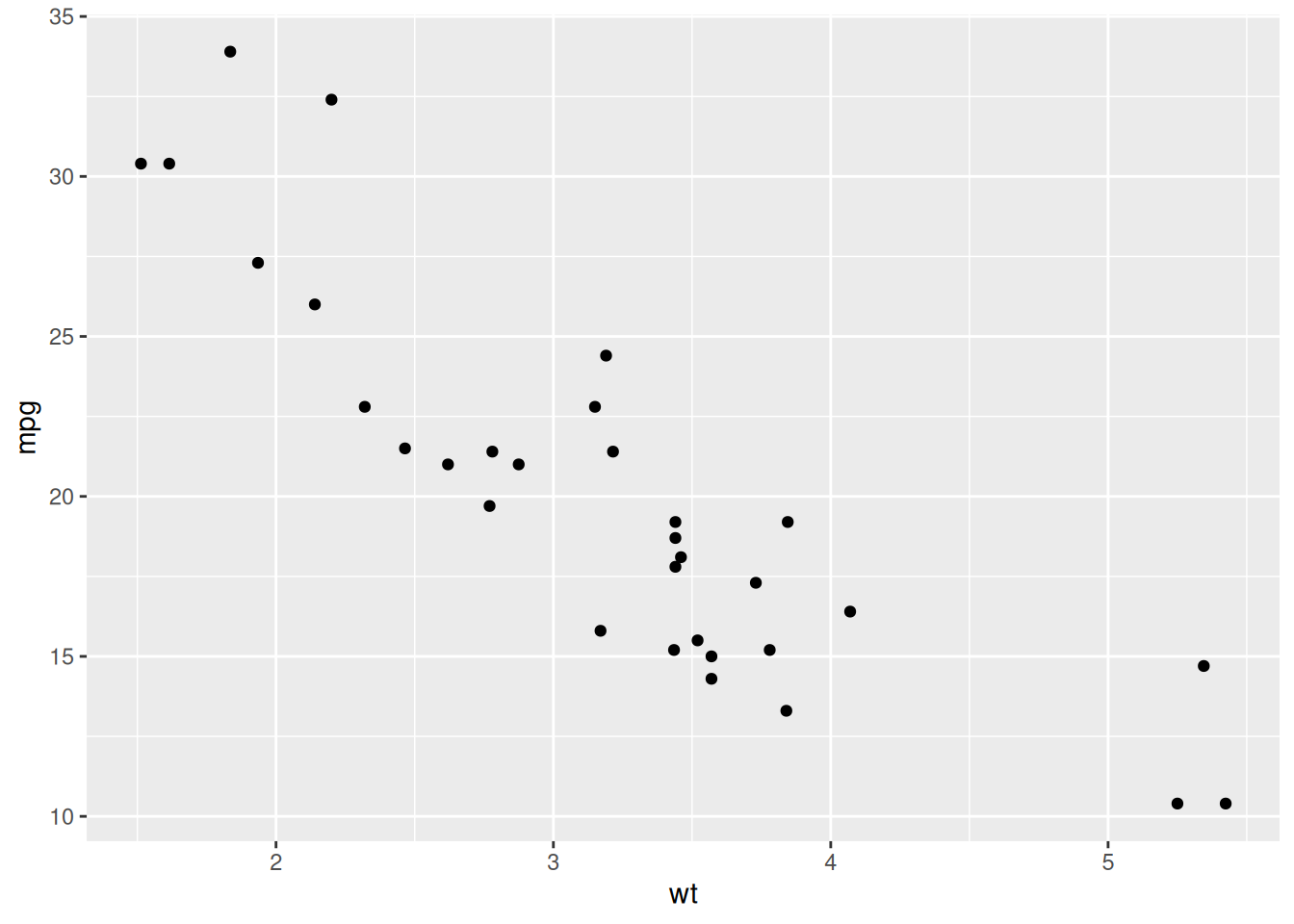

geo_point()	geom_bar()	geom_col()	stat_count()
geom_boxplot()	stat_boxplot()	geom_density()	stat_density()
geom_histogram()	geom_violin()

Quinto paso : Agregar caracteristicas adicionales

p <- ggplot(mtcars, aes(x = wt, y = mpg, color = cyl)) +
          geom_point(size = 2, alpha = 0.7)  # Tamaño y transparencia de los puntos
p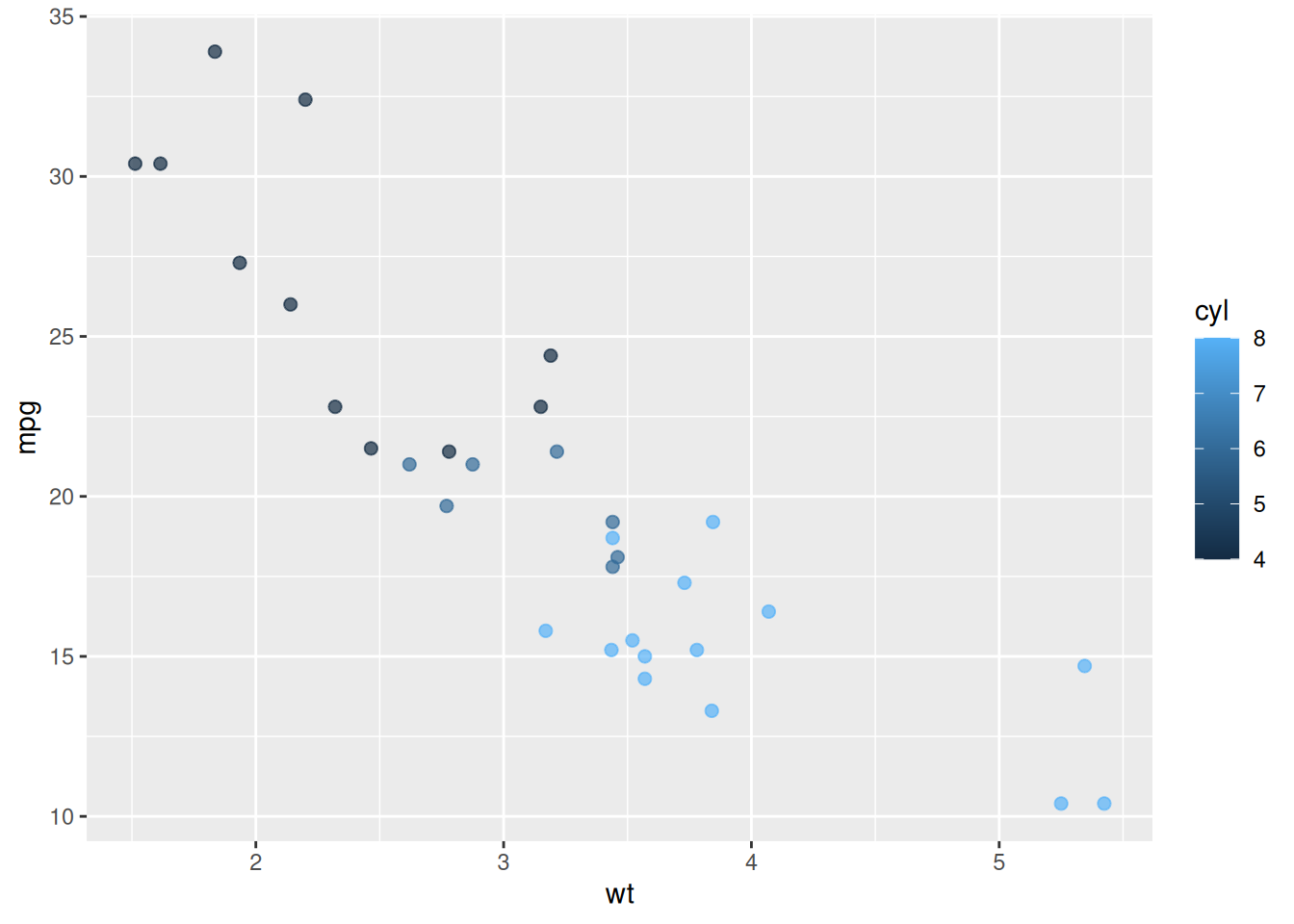

Paso sexto : Agregar títilo, etiquetas a los ejes leyenda aclararoria

p <- p + labs(title = "Relación entre Peso del Auto y Consumo de Combustible",
              subtitle = "Clasificación por número de cilindros",
              x = "Peso del Auto (1000 lbs)",
              y = "Millas por Galón (mpg)",
              color = "Cilindros"
              )
p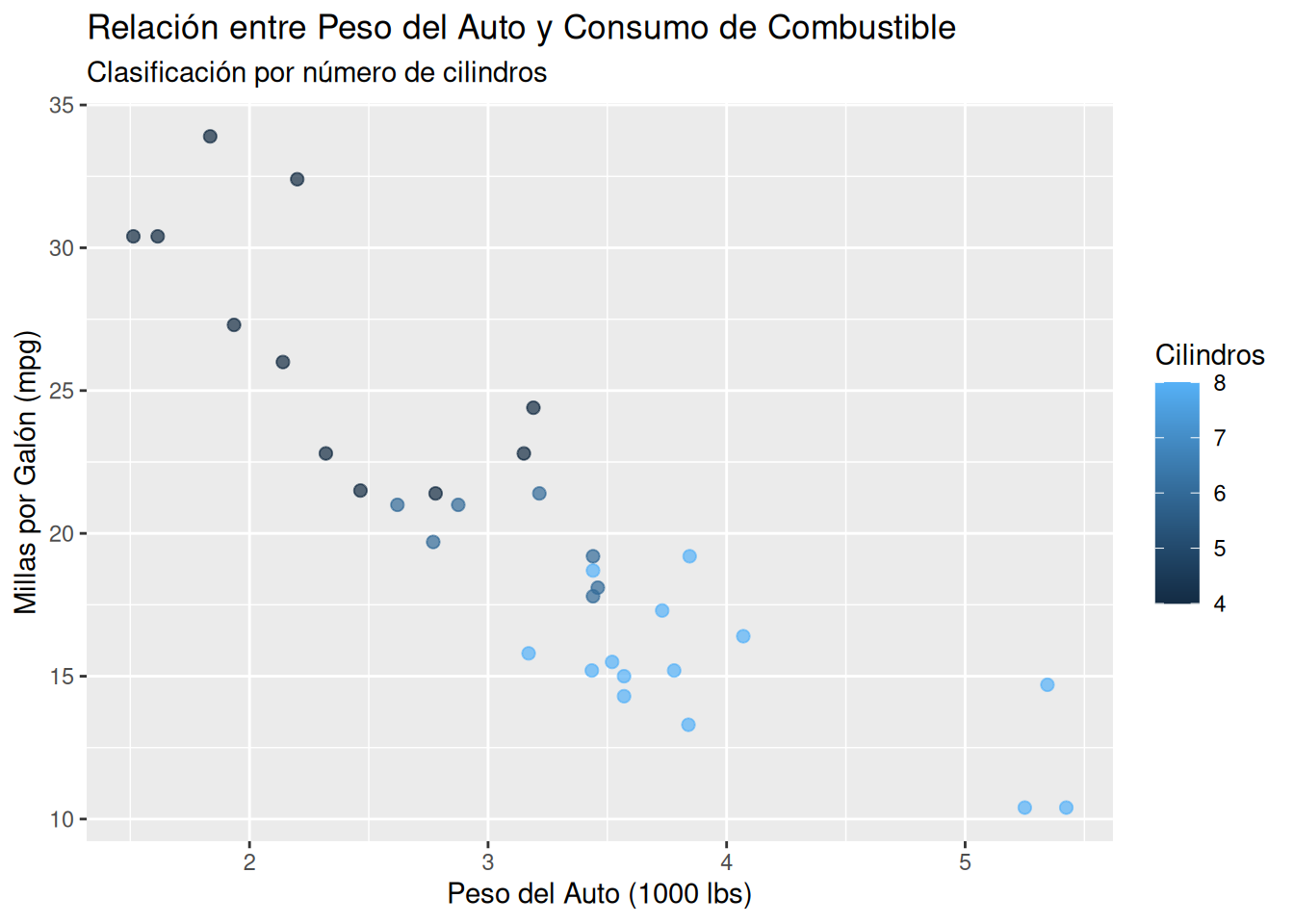

Septimo paso : Agregar una línea de tendencia

p <- p + geom_smooth(method = "lm", se = FALSE, linetype = "dashed", color = "black")
p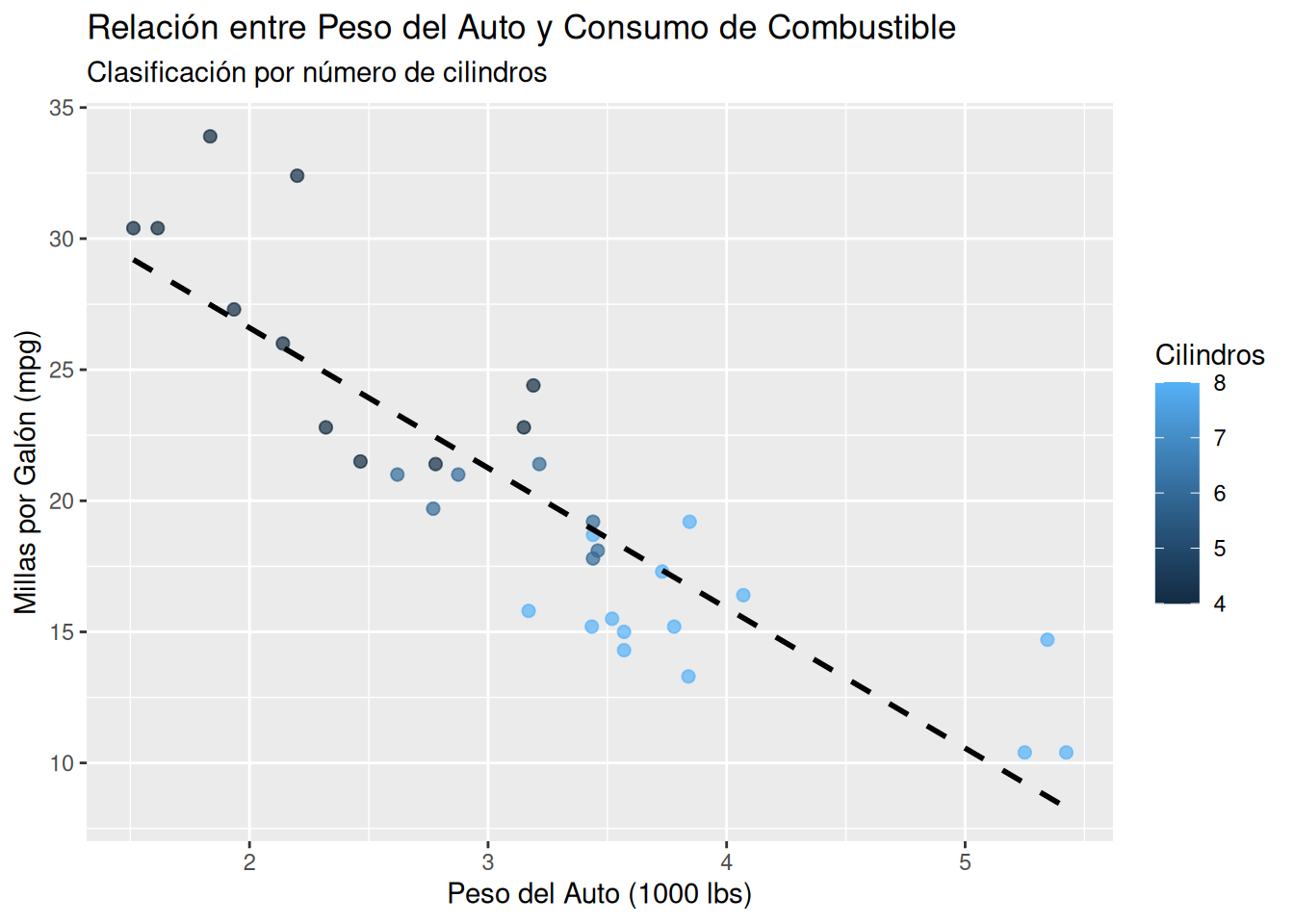

Octavo paso : Agreagar un tema o fondo

p <- p + theme_minimal(base_size = 14)
p

`geom_smooth()` using formula
= 'y ~ x'

Noveno paso : Ajustar la escala de colores

library(ggplot2)

# Asegurar que cyl es un factor
mtcars$cyl <- as.factor(mtcars$cyl)

# Crear el gráfico desde cero
p <- ggplot(mtcars, aes(x = wt, y = mpg, color = cyl)) +
  geom_point(size = 4, alpha = 0.7) +  # Agregar puntos
  scale_color_brewer(palette = "Set1") +  # Aplicar escala de color discreta
  labs(
    title = "Relación entre Peso y Consumo de Combustible",
    subtitle = "Clasificación por número de cilindros",
    x = "Peso del Auto (1000 lbs)",
    y = "Millas por Galón (mpg)",
    color = "Cilindros"
  ) +
  theme_minimal(base_size = 14)

# Mostrar el gráfico
p

Otros gráficos

library(ggplot2)
data=data.frame(carrera=c("biologia","biomedica","civil","electronica","mecanica",  "sistemas"),frecuencia=c(8, 9,10,2, 3,7))

ggplot(data, aes(x=carrera, y=frecuencia)) +
  geom_bar(stat="identity", fill="#203c3d")+
  geom_text(aes(label=frecuencia), vjust=2.5, color="white", size=7)+
  theme_minimal()

ggplot(iris, aes(Sepal.Length)) +
       geom_histogram(bins = 7,fill="#447270", color="#e9ecef", alpha=0.9)+
       theme_minimal() +
       labs(x = "cm", y = "frecuencia absoluta") +
       ggtitle("Longitud del sepalo")

ggplot(iris, aes(x=Sepal.Length, y=Species)) +
  geom_boxplot(fill=c("#faf0ca","#f4d35e","#ee964d"),  # color de relleno
               color="#0d3b66",    # color de lineas
               alpha=0.5)+
  geom_point(color="#2C5697",alpha=0.2)     # color puntos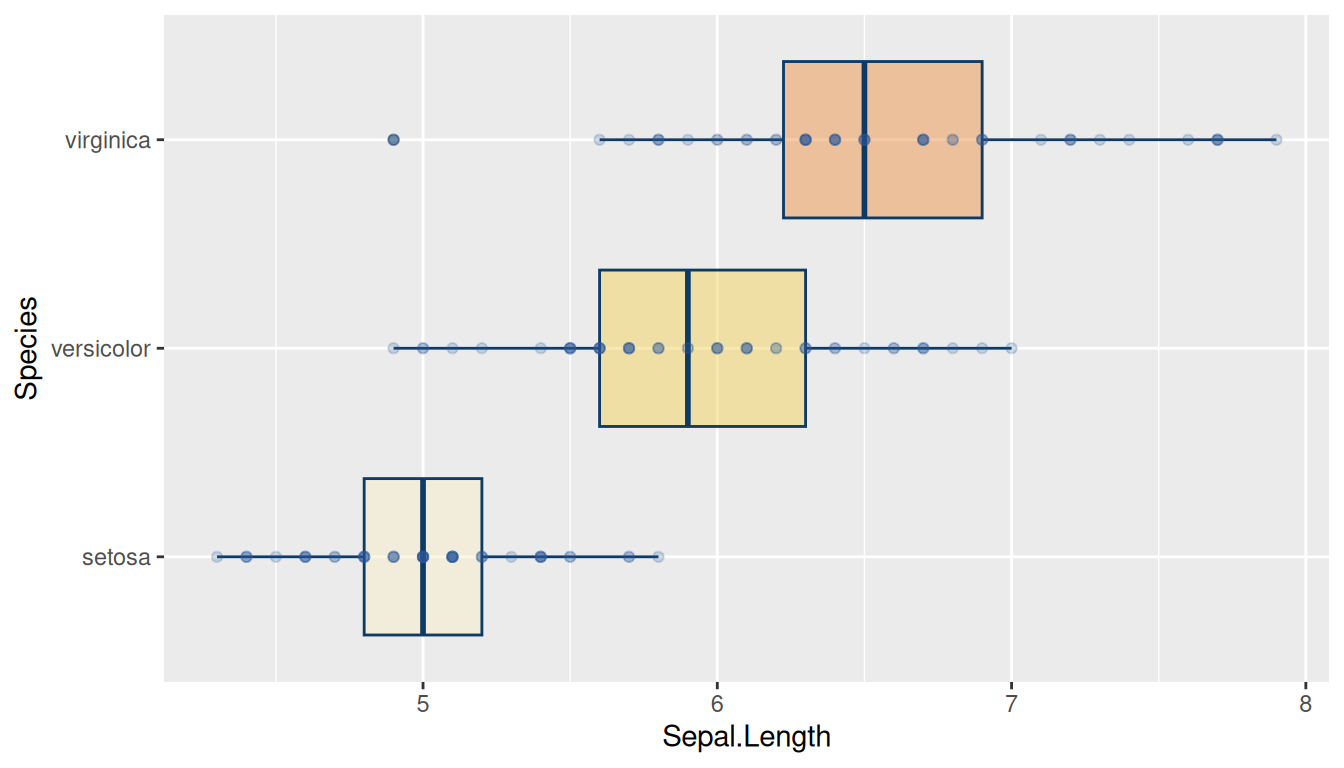

Gráficos con plotly

# Instalar paquetes si es necesario
# install.packages("plotly")

# Cargar librerías necesarias
library(ggplot2)
library(plotly)

# Convertir 'cyl' a factor para que se represente como variable categórica
mtcars$cyl <- as.factor(mtcars$cyl)

# Crear gráfico base con ggplot2
p <- ggplot(mtcars, aes(
  x = wt, y = mpg, color = cyl,
  text = paste(
    "Modelo:", rownames(mtcars), "<br>",
    "Peso (wt):", wt, "<br>",
    "Millas por Galón (mpg):", mpg, "<br>",
    "Cilindros:", cyl
  )
)) +
  geom_point(size = 2, alpha = 0.7) +  # Agregar puntos
  scale_color_brewer(palette = "Set1") +  # Escala de color
  labs(
    title = "Relación entre Peso y Consumo de Combustible",
    subtitle = "Datos de mtcars",
    x = "Peso del Auto (1000 lbs)",
    y = "Millas por Galón (mpg)",
    color = "Cilindros"
  ) +
  theme_minimal(base_size = 14)

# Convertir el gráfico de ggplot2 a un gráfico interactivo con Plotly
p_interactivo <- ggplotly(p, tooltip = "text")

# Mostrar el gráfico interactivo
p_interactivo

https://gganimate.com/

Anàlisis de datos con R Cap,7 ggplot2
ggplot2 resumen

Graficos con highcharter

# Instalar paquetes si es necesario
# install.packages("highcharter")
# install.packages("dplyr")

# Cargar librerías necesarias
library(highcharter)
library(dplyr)

# Convertir 'cyl' a factor para diferenciar los colores
mtcars <- mtcars %>%
  mutate(
    cyl = as.factor(cyl),  # Convertir a factor
    modelo = rownames(mtcars)  # Guardar nombres de los autos
  )

# Crear gráfico interactivo con highcharter
hchart(mtcars, "scatter", hcaes(x = wt, y = mpg, group = cyl, name = modelo)) %>%
  hc_title(text = "Relación entre Peso y Consumo de Combustible") %>%
  hc_subtitle(text = "Datos de mtcars con diferenciación por cilindros") %>%
  hc_xAxis(title = list(text = "Peso del Auto (1000 lbs)")) %>%
  hc_yAxis(title = list(text = "Millas por Galón (mpg)")) %>%
  hc_tooltip(
    useHTML = TRUE,
    pointFormat = "<b>Modelo:</b> {point.name}<br>
                   <b>Peso (wt):</b> {point.x}<br>
                   <b>Millas por Galón (mpg):</b> {point.y}<br>
                   <b>Cilindros:</b> {point.group}"
  ) %>%
  hc_chart(zoomType = "xy")

Graficos con Shiny

RMarkdown

RMarkdown resumen

R flexdashboard - ejemplo
R flexdashboard - implementaciòn

Estética en la visualización

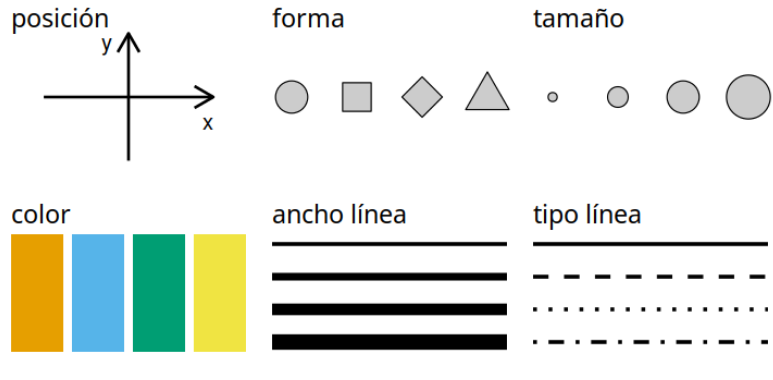
La estética juega un papel fundamental en la visualización de datos, ya que ayuda a hacer que la información sea más comprensible y atractiva para el espectador. Entre las diferentes formas de estética utilizadas en la visualización, se encuentran:

Forma
Tamaño
Color
Ancho línea
Tipo línea
1D, 2D, 3D

La posición se refiere a la ubicación de los elementos dentro de la visualización y es fundamental para transmitir información espacial. Por lo general haciendo referencia al plano cartesiano (2D) e indicando relaciones de asociación y correlación entre variables.

La forma se refiere a la apariencia de los elementos, que puede ser útil para representar categorías o para resaltar ciertos datos, como pueden ser: circulos, cuadrados, triangulos, estrellas, entre otras formas.

El tamaño, por otro lado, se utiliza para indicar magnitudes y hacer que ciertos elementos destaquen sobre otros.

El color es una de las estéticas más poderosas en la visualización, ya que puede transmitir información de manera rápida y efectiva. Se puede utilizar para representar categorías, resaltar elementos importantes o crear jerarquías visuales. Tambien reforzando el significado de la variable, por ejemplo en presentación de resultados de clima laboral se utilizan colores relacionados con el semaforo (escalas entre rojo y verde), para representar magnitudes desde colores suaves a colores fuertes para indicar grandes cantidades. Por último tambien se emplean colores para resaltar un nivel u objeto dentro de todo el grupo.

El ancho de línea y el tipo de línea se utilizan para diferenciar entre elementos y resaltar ciertos aspectos de la visualización.

La dimensión (1D, 2D, 3D) se refiere a la cantidad de dimensiones que se utilizan en la visualización. Mientras que las visualizaciones 1D se limitan a una sola dimensión, como una línea de tiempo, las visualizaciones 2D y 3D pueden representar información en dos o tres dimensiones, lo que permite una representación más detallada y compleja de los datos. Es recomendable no utilizar 3D para que las visializaciones sean más limpias y sencillas

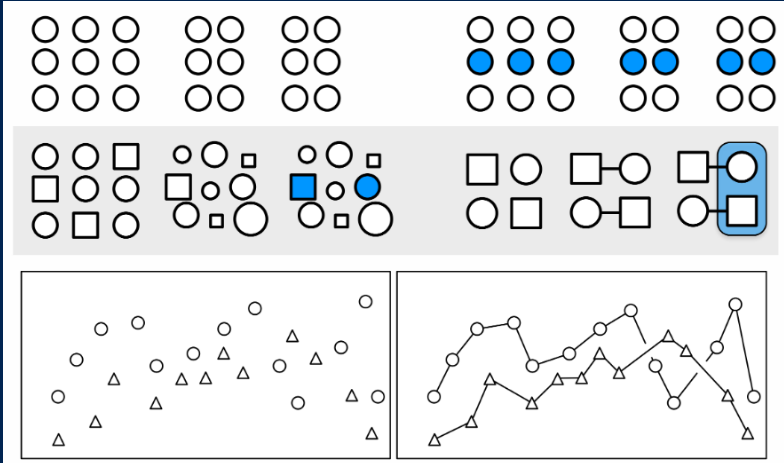
Formas

Es posible utilizar circulos, cuadrados, triangulos y en general figuras geométricas para resaltar puntos que represente valores numéricos en un plano 2D y de esta forma representar una secuencia o tendencia de la información.

Paletas

Normas EEEE

Las normas EEEE para la construcción de gráficos son principios fundamentales en la visualización de datos que garantizan claridad, precisión y eficacia en la comunicación. Estas normas son:

Eficiencia:

El gráfico debe transmitir la información de manera rápida y clara. Evita decoraciones innecesarias (chartjunk). Usa escalas adecuadas para facilitar la interpretación.

Eficacia:

El gráfico debe cumplir con su propósito comunicativo. Elige el tipo de gráfico más adecuado para los datos (barras, líneas, dispersión, etc.). Usa etiquetas, títulos y leyendas para orientar al lector.

Exactitud:

Representa los datos de forma fiel y sin distorsiones. Usa escalas proporcionales y evita manipulaciones visuales que alteren la percepción. Si se usan porcentajes, asegúrate de que la suma sea 100%.

Estética:

El diseño debe ser limpio y atractivo sin afectar la legibilidad. Usa colores adecuados con suficiente contraste. Mantén coherencia en los estilos y fuentes. Siguiendo estas normas, se logra que los gráficos sean interpretados correctamente y comuniquen la información de manera efectiva

ggplot(cars, aes(x = speed)) +
  geom_histogram(fill = "steelblue", bins = 10, color = "black", alpha = 0.7) +
  labs(
    title = "Distribución de la Velocidad de los Automóviles",
    x = "Velocidad (mph)",
    y = "Frecuencia",
    caption = "Fuente: Base de Datos 'cars' de R"
  ) +
  theme_minimal()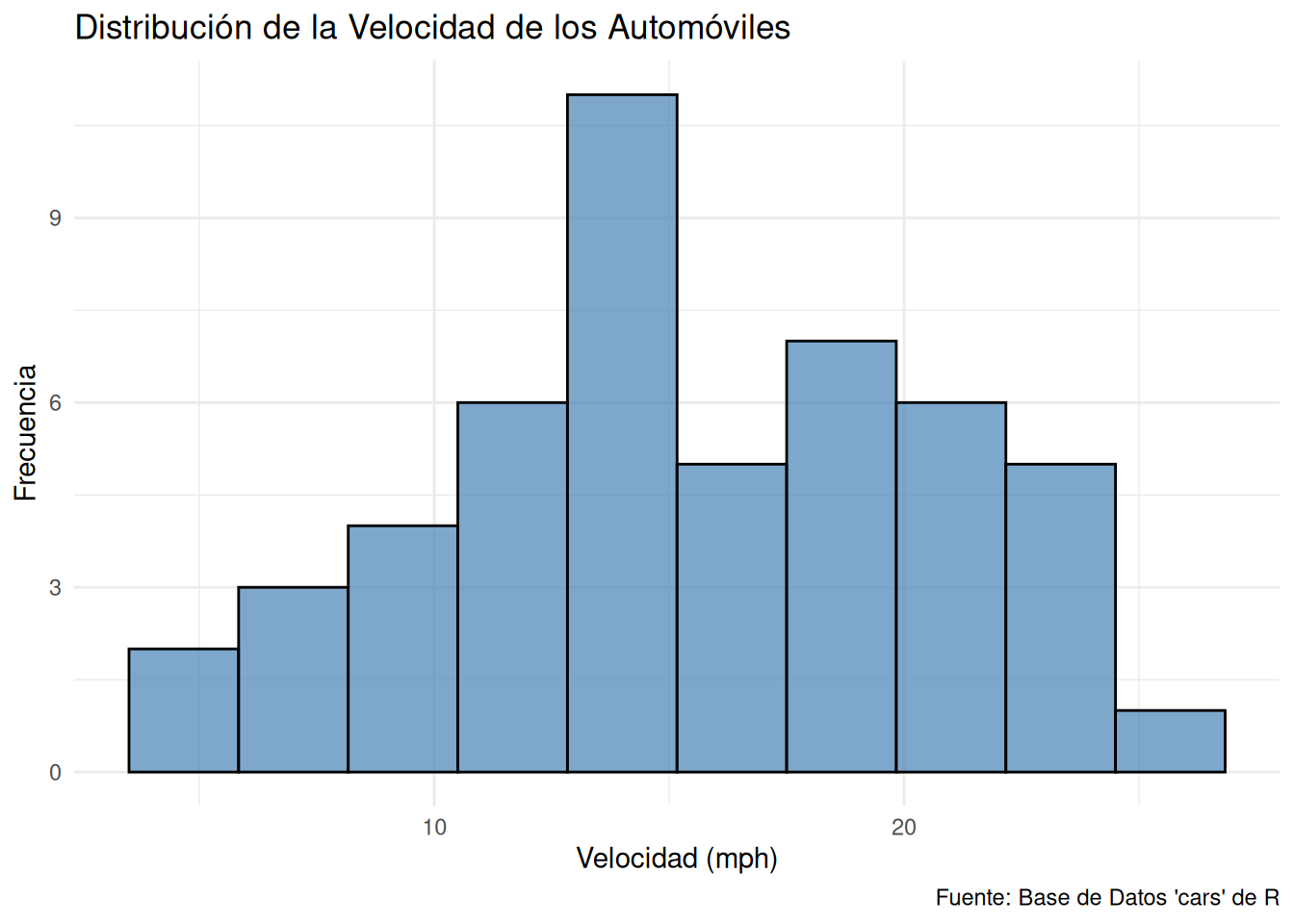

ggplot(cars, aes(x = speed, y = dist)) +
  geom_point(color = "darkred", size = 2, alpha = 0.7) +
  geom_smooth(method = "lm", se = FALSE, color = "black", linetype = "dashed") +
  labs(
    title = "Relación entre Velocidad y Distancia de Frenado",
    x = "Velocidad (mph)",
    y = "Distancia de Frenado (ft)",
    caption = "Fuente: Base de Datos 'cars' de R"
  ) +
  theme_minimal()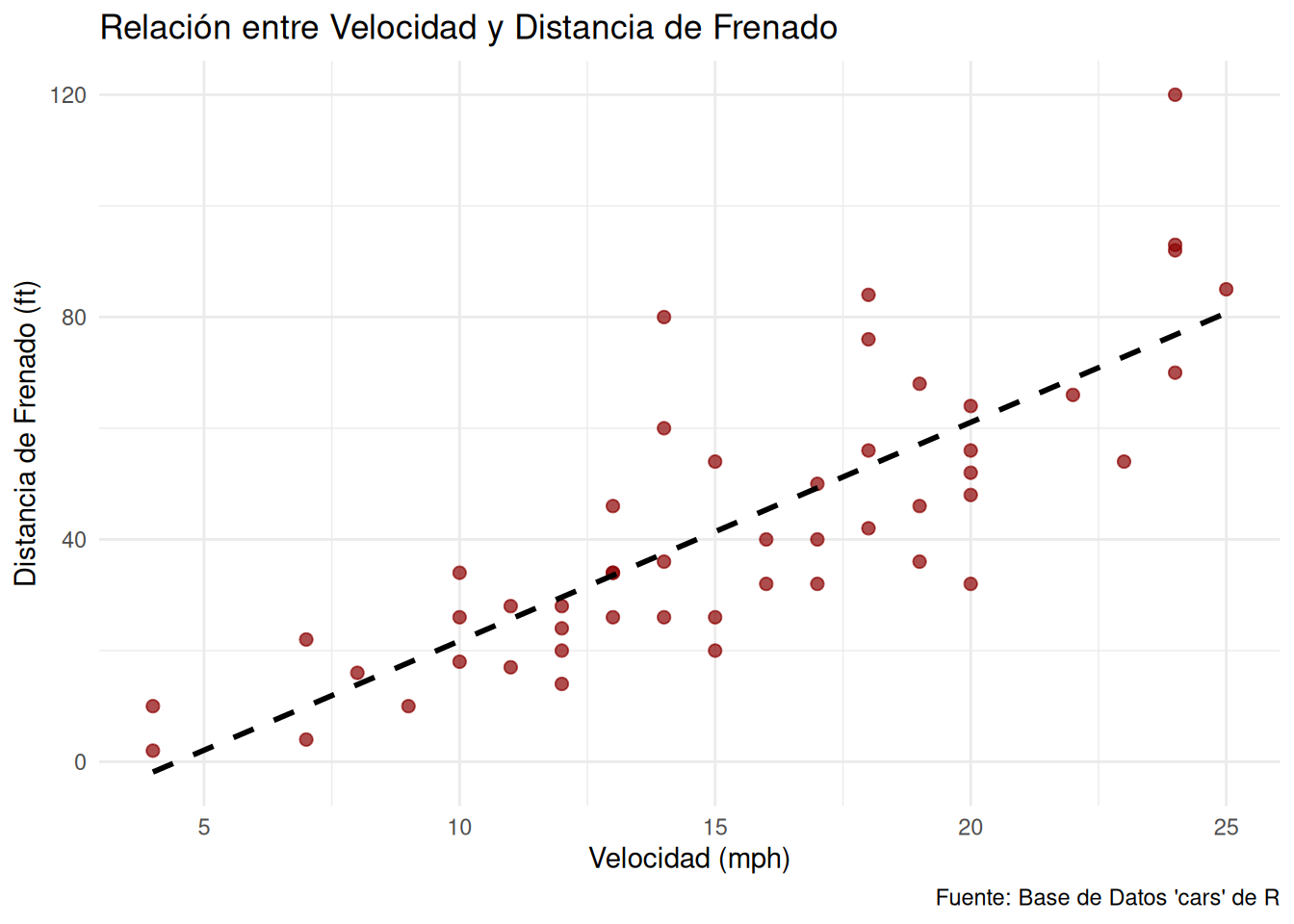

Una imagen dice mas que mil palabras…

Daniel Enrique González Gómez

Imagen tomada de :https://javerianacali.edu.co/noticias/la-javeriana-bogota-y-cali-1-de-colombia

Unidad 1.1

dgonzalez

Introducción

Paquetes de R para gráficos

Gráficos variables cualitativas con R base

Diagrama de barras

Diagrama de barras dos variables

Gráficas variables cuantitativas con R base

Diagrama de árbol

Histograma

Diagrama de densidad

Diagrama de cajas

Diagrama de cajas

Diagrama de dispersión

Gráfica de series de tiempo

Resumen

Gráficos con ggplot2

Primer paso: Instalar y cargar la libreria

Segundo paso : Declarar la base de datos y las varibles

Cuarto paso : Crear grafico base con las diferentes geometrías

Quinto paso : Agregar caracteristicas adicionales

Paso sexto : Agregar títilo, etiquetas a los ejes leyenda aclararoria

Septimo paso : Agregar una línea de tendencia

Octavo paso : Agreagar un tema o fondo

Noveno paso : Ajustar la escala de colores

Otros gráficos

Gráficos con plotly

Graficos con highcharter

Graficos con Shiny

RMarkdown

Estética en la visualización

Formas

Paletas

Normas EEEE

Eficiencia:

Eficacia:

Exactitud:

Estética:

Una imagen dice mas que mil palabras…