Módulo 3
dgonzalez

Taller 431
punto 1
Suponga que se estudia la compra de una nueva maquina para una empresa. Se comprará si la proporción de la producción que necesita ser reprecesados por tener defectos es inferior al 5%. Se examina una muestra de 40 artículos construidos por la máquina y 3 necesitan ser reprocesados. ¿Que decisión se toma? (Se compra o no la máquina?)
punto 2
Suponga que una empresa desarrolla un curso de entrenamiento
para sus empleados, formando dos grupos y aplicándoles dos métodos
distintos de entrenamiento. El primer grupo lo componen 36 empleados,
mientras que el segundo grupo por 40 empleados. Los resultados en
calificaciones entre 0 y 10, se presentan a continuación:
grupos : n media varianza grupo 1 : 36 7.125 1.415643 grupo 1 : 40 8.075 0.9798718 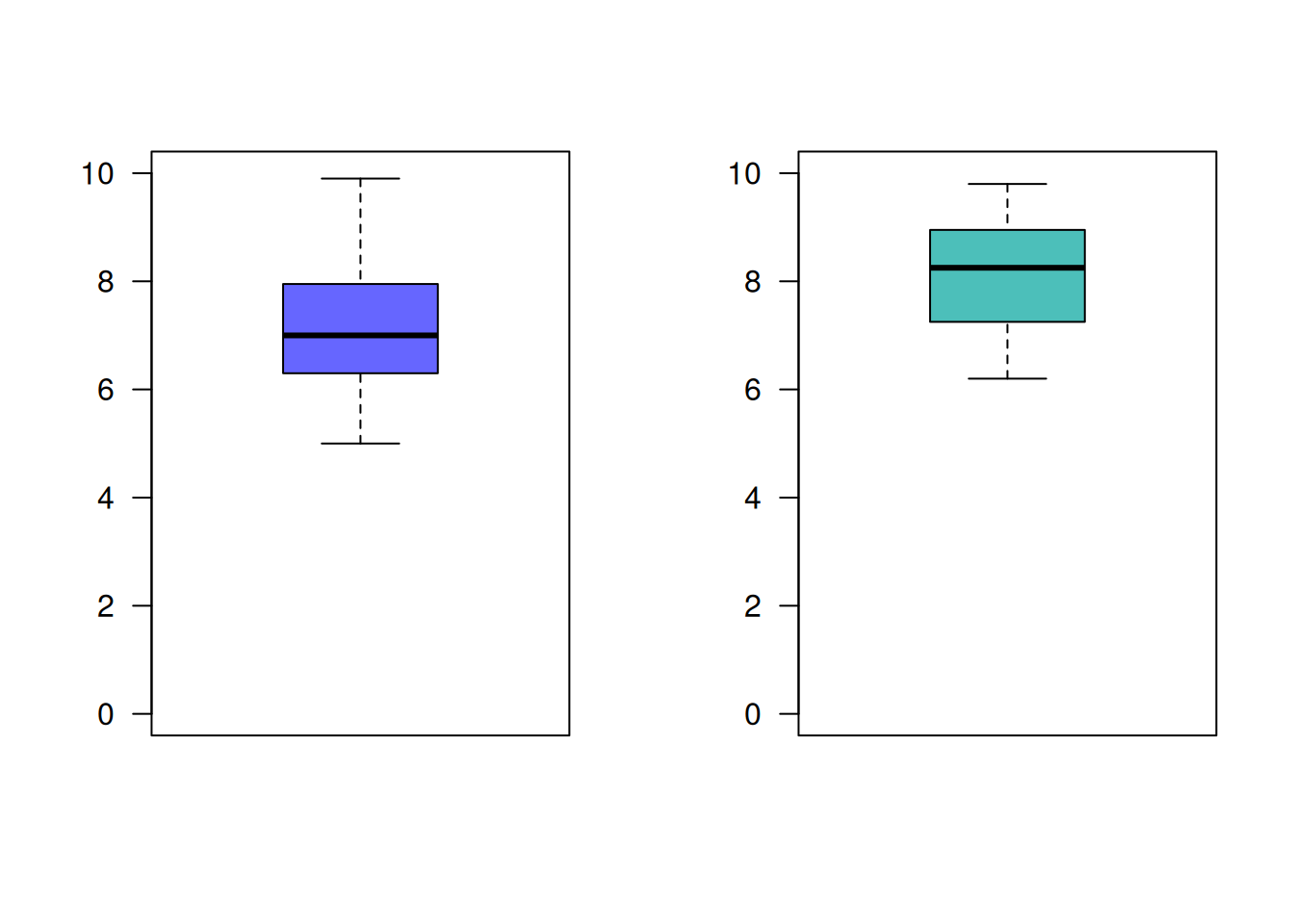
punto 3
Los ingenieros de una ensambladora de automóviles requieren decidir sobre cual de dos de las marcas de neumáticos de deben comprar. La marca FB o la marca KT. Con el fin de tomar una decisión basada en evidencias estadísticas, deciden realizar un experimento en el que usan 12 neumáticos de cada marca. Los neumáticos se utilizan hasta su terminación . Los resultados obtenidos (en miles de kilometros) se presentan a continuación :
marcas : n media varianza FB : 12 37.20833 29.33902 KT : 12 41.66667 12.13879 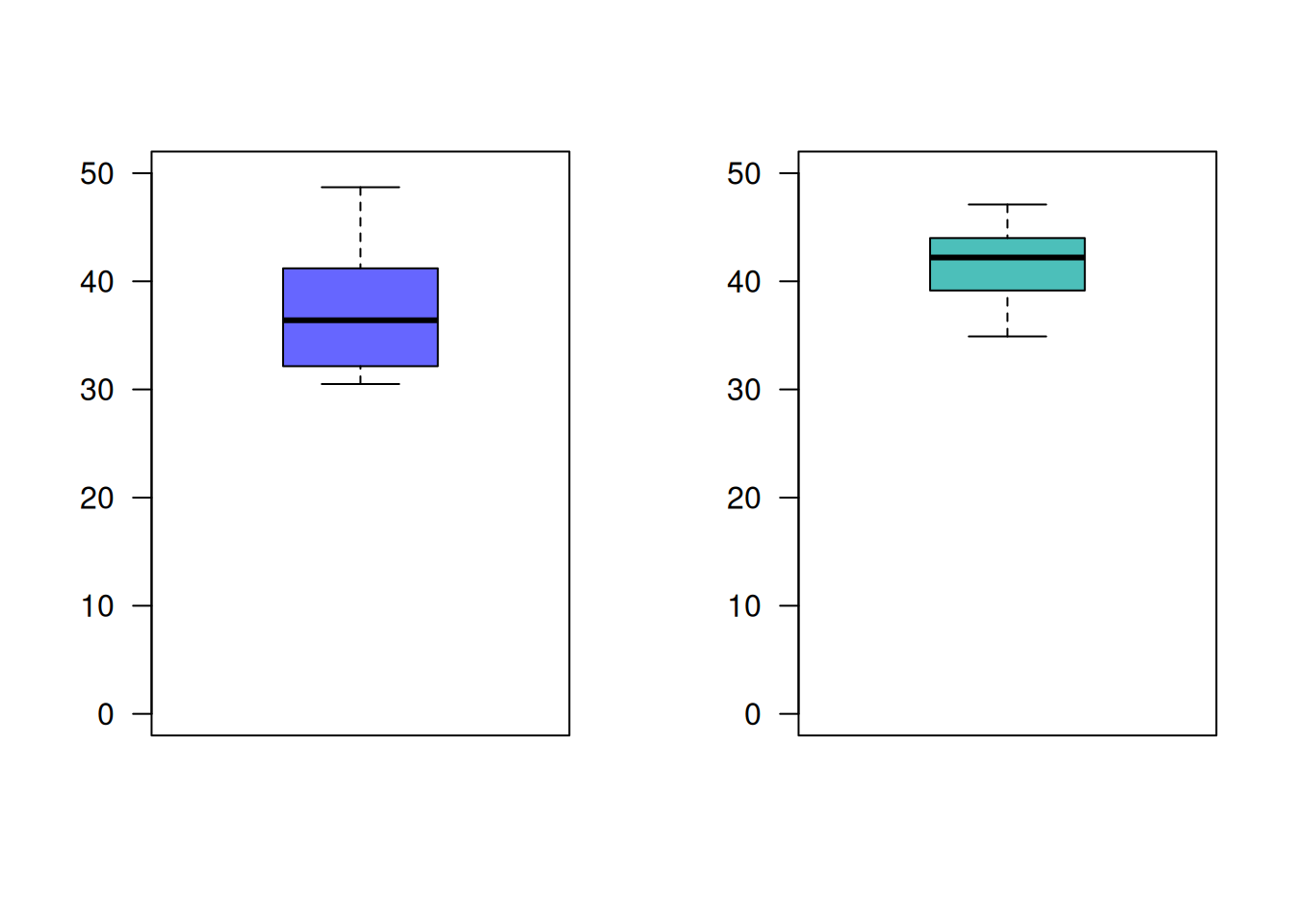
¿Cual de las marcas de neumáticos recomendaría comprar? ¿Que supuestos deberá confirmar?. Utilice un \(\alpha=0.05\)
punto 4
Un ingeniero desea establecer si existen diferencias entre dos métodos diferentes de realizar el ensamble de una casa prefabricada. Para comprobarlo recogen información del tiempo empleado en el ensamble de una pieza para ambos métodos en horas, los cuales se presentan a continuación:
métodos : n media varianza nuevo : 9 35.22222 24.44444 estandar : 9 31.55556 20.02778 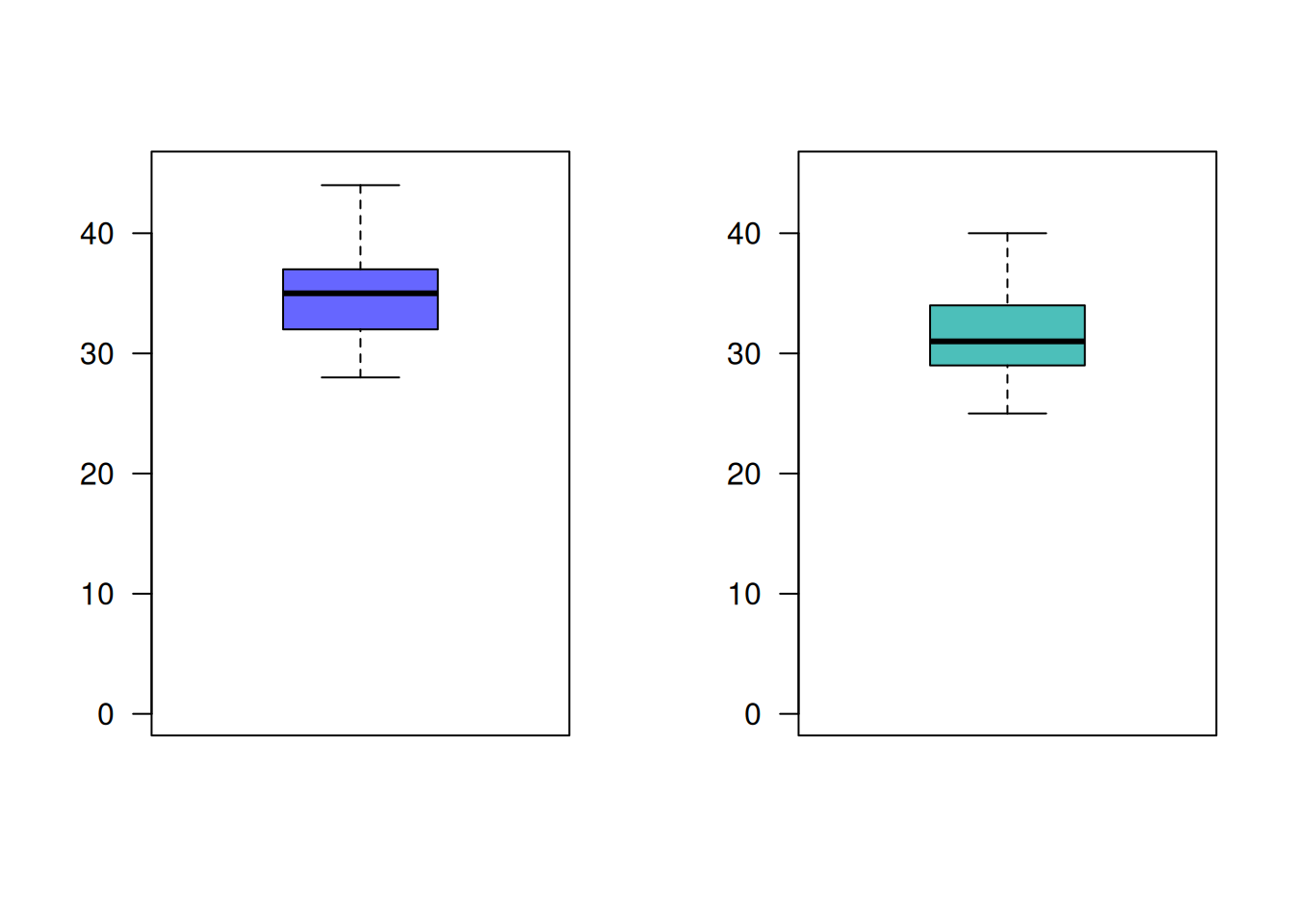
Presentan los datos suficiente evidencia que permita afirmar que el nuevo método es mas eficiente que el método estándar? (Utilice un \(\alpha=0.05\))
punto 5
El director de un gimnasio quiere determinar si un instructor de ejercicios debe ser contratado o no para su campaña estrella “Reducción de peso”. Para tomar la decisión indica a un candidato que pruebe con 16 personas que asisten habitualmente al gimnasio. Los siguientes datos corresponden a los pesos tomados al inicio del programa (\(x1\)) y sus pesos al finalizar el programa (\(x2\))
[1] 6 4 -1 3 2 1 0 0 3 0 2 1 1 3 10 2tiempo : n media varianza inicio : 16 2.3125 7.295833 ¿Que supuestos se deben verificar? ¿Se podría decir que las rutinas empleadas por el instructor producen los efectos indicados?
punto 6
Se realizan pruebas de un nuevo lector láser manual para uso en la realización de inventarios y del lector utilizado actualmente, con el fin de decidir si se adquiere el primero. Se obtienen los datos sobre el número de códigos de barra leídos por segundo con el cada uno de los dispositivos.
instrumento : n media varianza nuevo : 61 40.5082 27.1541 actual : 61 29.54098 17.61913 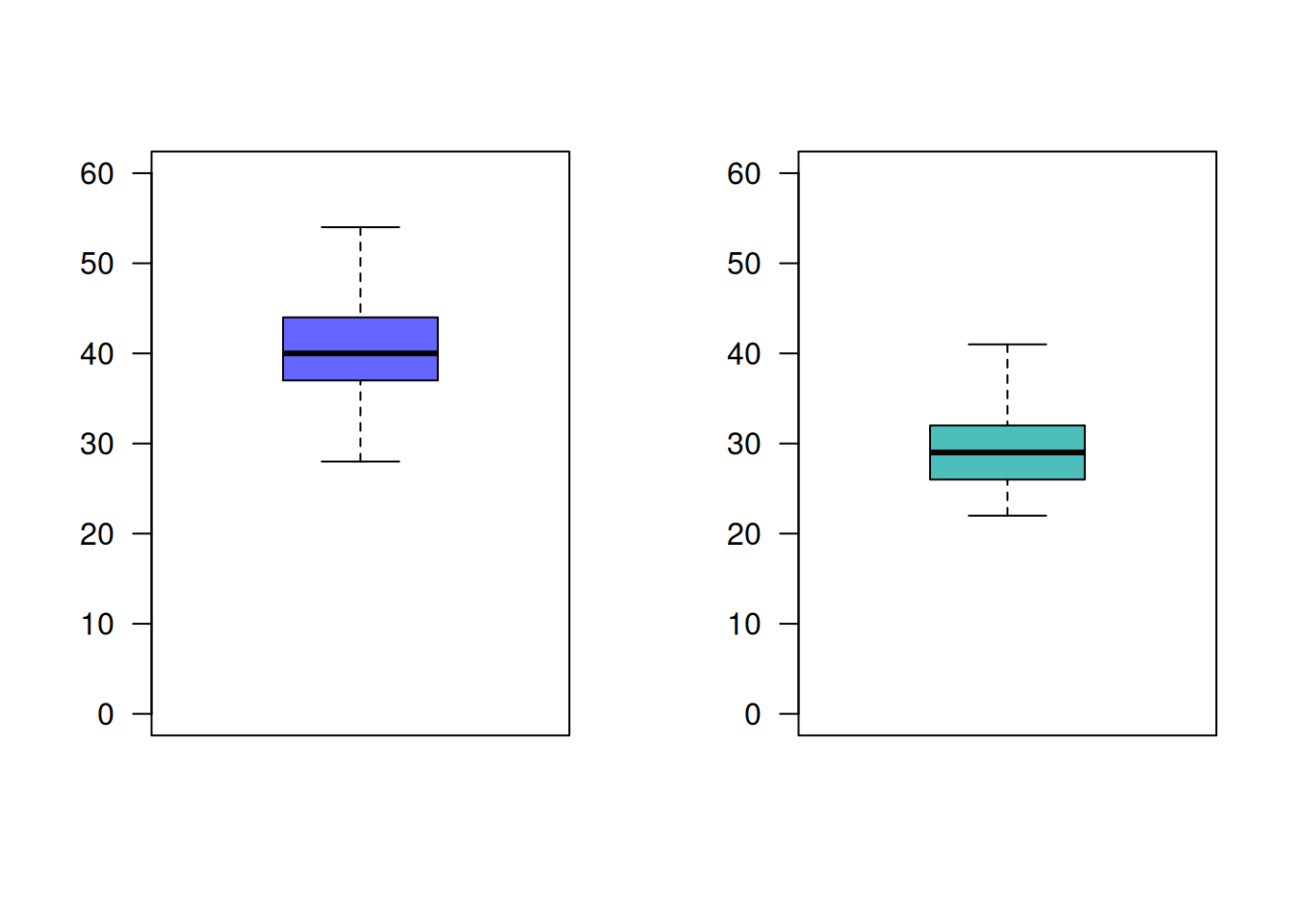
De acuerdo con la información, es posible preferir alguno de ellos? ¿Que supuestos se deben verificar?
punto 7
Un empresario registro el número de artículos producidos durante 10 días para un grupo conformado por 15 obreros los cuales tienen un salario fijo (grupo 1). El gerente piensa que si se cambia la forma del salario tendrán mejores resultados. Para verificarlo introduce cambios en la forma de pago a un segundo grupo (grupo 2) . El numero de artículos producidos por ambos grupos son los siguientes:
grupos : n media varianza grupo 1 : 10 75.1 6.544444 grupo 2 : 10 82.4 13.37778 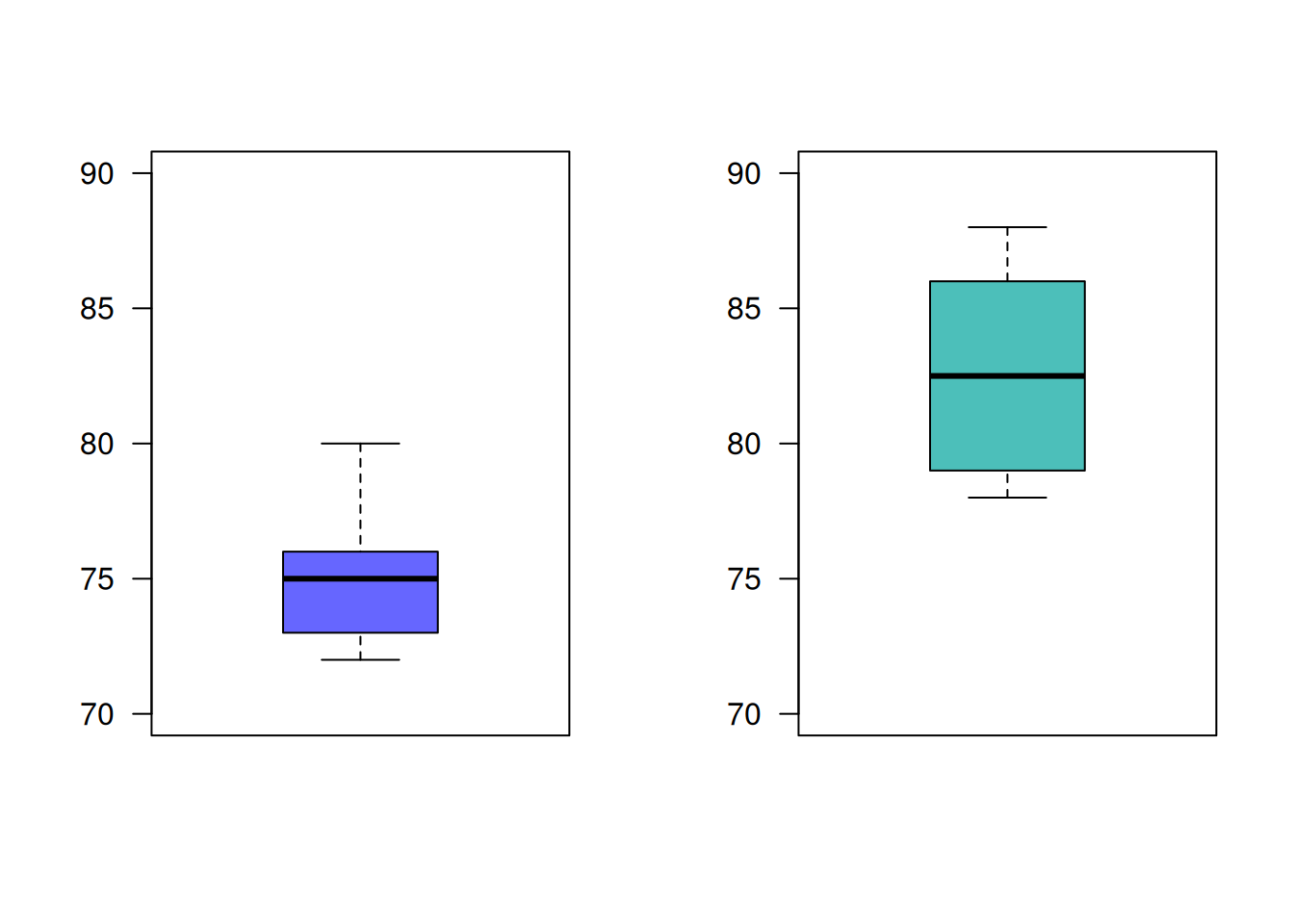
Suponiendo que los salarios pagados a ambos grupos son equivalentes, se podría afirmar que el plan de incentivos es efectivo? ¿Que supuestos se deben verificar?
punto 8
La pizzeria P20 realizó el mes pasado una encuestas (\(n_1=200\)) para determinar la proporción de clientes que prefieren el tamaño familiar. La encuesta recogida muestra que el 20% de sus clientes prefieren el tamaño familiar. Con el fin de aumentar las ventas, realiza una estrategia de publicidad en redes. Pasado dos meses de la campaña la empresa realizó una segunda encuesta (\(n_2=200\)), obteniendo en este caso una proporción de 25%.
De acuerdo con los resultados podría decirse que la campaña realizada es efectiva? (utilice un \(\alpha=0.05\))
# prop.test(c(40,50), c(200,200), conf.level = 0.95)Taller 432
punto 1
Se lanza una moneda hasta que sale una cara y se reguistra el número de lanzamientos \(X\). Depués de repetir el experimento 256 veces, se observan los siguientes resultados:
| \(x\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| \(f(x)\) | 136 | 60 | 34 | 12 | 9 | 1 | 3 | 1 |
A un nivel de significancia de \(0.05\) pruebe la hipótesis de que la
distribución observada de \(X\) se
puede ajustar a una distribución geometrica geom(x, 0.50),
para \(x=1,2,3,4,5....\)
punto 2
Una muestra aleatoria de 90 adultos se ckasifica de acuerdo al genero y el número de horas que dedica a ver la televisión durante una semana:
| genero | Masculino | Femenino |
|---|---|---|
| más de 25 horas | 15 | 29 |
| menos de 25 horas | 27 | 19 |
Utilice un nivel de significancia del \(0.01\) y pruebe la hipótesis de que el tiempo dedicado a ver televisión es independiente de si el espectador es hombre o mujer.
punto 3
Un investigador realizó un estudio para determinar si la incidedencia de cierto tipo de delitos varia de una parte de una gran ciudad a otra. Los crímines específicos de interés eran el asalto, el robo de casas, el hurto y el homicidio. La siguiente tabla muestra el número de delitos cometidos en cuatro áreas de la ciudad durante el año pasado:
| Comuna | Asalto | Robo en casa | Hurto | Homicidio |
|---|---|---|---|---|
| 1 | 162 | 118 | 451 | 18 |
| 2 | 310 | 196 | 996 | 25 |
| 3 | 258 | 193 | 458 | 10 |
| 4 | 280 | 175 | 390 | 19 |
¿ A partir de los datos podemos concluir, a un nivel de significancia del \(0.01\) que la ocurrencia de estos topos de delitos dependen de la comuna de la ciudad?
punto 4
Se lleva a cobo una investigación en dos ciudades del Valle para determinar la opinión de los votantes respecto a dos candidatos a la presidencia paras proximas elecciones presidenciales. En cada cuidad se seleccionaron 500 personas votantes al azar y se registraron los siguientes datos :
| Opinión del votante | Ciudad 1 | Ciudad 2 |
|---|---|---|
| a favor de A | 204 | 225 |
| a favor de B | 211 | 198 |
| indeciso | 85 | 77 |
A un nivel de significancia del \(0.05\) pruebe la hipótesis nula de quelas las proporciones de votantes que estan a favor del candidato A, del candidato B o están indecisos son las mismas para cada ciudad.
punto 5
El departamento de Bienestar Universitario realizó un estudio para determinar si 8 semanes de entrenamiento realmente reducen los niveles de colesterol de los participantes . A un grupo de tratamiento que consta de 15 colaboradores se les dieron conferencias dos veces a la semana acerca de cómo reducir el nivel de colesterol. Otro grupo de 18 colaboradores de edad similar, fue seleccionado al azar como el grupo control. Se registraron los siguientes niveles de colesterol de todos los participantes del programa de 8 semanas.
Tratamiento:
129, 131,154,172, 115, 126, 175, 171, 122, 238, 159, 156, 176, 175, 126
Control:
151, 132, 196, 195, 188, 198, 187, 168, 115, 165, 137, 208, 133, 217, 191, 193, 140, 149
Actividad M&M
El sitio web de la compañía Mars publica los siguientes porcentajes de los distintos colores de sus dulces M&M para la variedad de chocolate candies de 49.3 g.

| café | amarillo | rojo | azul | naranja | verde |
|---|---|---|---|---|---|
| 13% | 14% | 13% | 24% | 20% | 16% |
Con la información recogia por los estudiantes en la hoja electrónica ubicada el sitio se puede afirmar que los datos obtenidos respaldan la información suministrada por la compañia en su pagina?. Use una prueba de hipótesis apropiada. Adjunte el proceso realizado
Taller 433
punto 1
Los jóvenes colombianos se ha vuelto más concientes con respecto a la importancia de una buena nutrición acompañada de actividad deportiva para tener una buena salud. Una asociación de profesionales relacionados con este tema opinan que los jóvenes están modificando sus dietas que incluyen menos carnes rojas y más frutas y verduras. Para vericar estas hipótesis un grupo de estudiantes de la universidad Javeriana de Cali decide seleccionar registros nutricionales de los estudiantes consignados en una encuesta realizada por Bienestar Universitario hace 10 años y comparar la cantidad promedio de carnes rojas consumidas por año con las cantidades consumidas por un grupo de jóvenes que serán entrevistados este año. De acuerdo con la información actual se estima que el consumo de carne de res por año varie entre 0 y 104 libras por año.
¿Cuánmtos jóvenes deben seleccionar los investigadores de cada grupo se desean estimar la diferencia en el consumo anual promedio per capita de carne de res correctamente dentro mas o menos 5 libras con una confianza del 99%?
Si además se desea estimar la proporción de jóvenes que son vegetarianos ¿qué tamaño deben tener en cuenta?
punto 2
Las investigadores del punto anterio selecionaron dos grupos de 400 jóvenes cada uno y reunieron la siguiente información sobre los hábitos de consumo de carne de res actuales y de hace 10 años.
| Hace 10 años | Este año | |
|---|---|---|
| media muestral (\(\bar{x}\)) | 73 | 63 |
| desviación estandar muestral (\(s\)) | 25 | 28 |
A los investigadores les gustaria poder mosrar que el consumo de carne percapita se redujo en los últomos 10 años, mediante a construcción de un intervalo de confianza. Con la información obtenida y el intervalo de confianza construido a qué conclusión se podría llegar?
punto 3
Uno de los problemas más frecuentes en los jóvenes universitarios es la alta tensión que generan las evaluaciones parciales, las cuales en algunos casos genera dolores de cabeza. La tensión muscular en la región de la cabeza se ha asociado con los dolores de cabeza. Es razonable pensar que so la tensión muscular disminuye, es probable que los dolores de cabezase reduzcan o desaparezcan. Un grupo de investigadores diseña un experimento en el cual participan nueve estudiantes que presentan dolores de cabeza durante la semana de evaluación (GE : Grupo experimental). Posteriormente un grupo de profesionales del Medio Universitrio los entrenan con el fin de que puedan aprender a reducir la tensión muscular en la tensión de la cabeza utilizando un dispositivode bioretroalaimentación. Para este experimento, el dispositivo mensionado se conecta en la región frontal de la cara. El dispositivo indica al estudiante la cantidad de tensión que existe en el musculo al cual está unido (en este caso al frontal) y le ayuda a reducir los niveles de tensión. Despues de 6 meses de entrenamiento, los jóvenes han logrado mantener baja la tensión en el musculo frontal; entonces se lleva nuevamente un registro de los dolores de cabeza que sufren durante las dos semanan de evaluaciones. La información recogida se muestra a continuación:
| Sujeto | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| \(GE_A\) | 17 | 13 | 6 | 5 | 5 | 10 | 8 | 9 | 7 |
| \(GE_D\) | 3 | 7 | 2 | 3 | 6 | 2 | 1 | 0 | 2 |
| Sujeto | GEa | GEd |
|---|---|---|
| 1 | 17 | 3 |
| 2 | 13 | 7 |
| 3 | 6 | 2 |
| 4 | 5 | 3 |
| 5 | 5 | 6 |
| 6 | 10 | 2 |
| 7 | 8 | 1 |
| 8 | 9 | 0 |
| 9 | 7 | 2 |
- \(GE_A\) : Grupo experimental antes
- \(GE_D\) : Grupo experimental después del entrenamiento
Dado que pueden existir problemas ede interpretación en el planteamiento anterior, debido a que los resultados aparentemente muestra una disminución de los dolores de cabeza, es posible que esta disminución no se deba al entrenamiento realizado con la utilización del dispositivo, sino a algún otro factor tambien presente en la situación, como por ejemplo el momento en que se realizan las mediciones (primeros parciales, segundos parciales, examenes finales), los investigadores incorporan un grupo que se denomina grupo control (GC ). Este segundo grupo que también presenta dolores de cabeza fue medido durante los mismos momentos del primer grupo (GE). Durante el periodo intermendio el grupo control no fue entrenado con el dispositivo para controlar la tensión . El número de dolores de cabeza para el segundo grupo (GC) durante los dos momentos son los siguiente
| Sujeto | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| \(GC_A\) | 5 | 8 | 14 | 16 | 6 | 5 | 8 | 10 | 9 |
| \(GC_D\) | 4 | 9 | 12 | 15 | 4 | 3 | 7 | 6 | 7 |
| Sujeto | GCa | GCd |
|---|---|---|
| 1 | 5 | 4 |
| 2 | 8 | 9 |
| 3 | 14 | 12 |
| 4 | 16 | 15 |
| 5 | 6 | 4 |
| 6 | 5 | 3 |
| 7 | 8 | 7 |
| 8 | 10 | 6 |
| 9 | 9 | 7 |
Se puede concluir que el entrenamiento realizado con el dispositivo disminuye los dolores de cabeza?
Nota:
Suponga que el número de dolores de cabeza se distribuye aproximadamente normal.
Tomado de Roberto Pangano (2006).
Formulario
| parámetro | intervalo de confianza | |
|---|---|---|
| media | \[IC_{\mu}: \bar{x} \pm z_{\alpha/2} \hspace{.1cm}\frac{\sigma}{\sqrt{n}}\] | (1) |
| \[IC_{\mu}: \bar{x} \pm z_{\alpha/2} \hspace{.1cm}\frac{s}{\sqrt{n}}\] | (2) | |
| \[IC_{\mu}: \bar{x} \pm t_{\alpha/2; v=n-1} \hspace{.1cm}\frac{s}{\sqrt{n}}\] | (3) | |
| tamaño muestra | \[n = \displaystyle\frac{z_{\alpha/2}^{2}\sigma^{2}}{e^{2}}\] | (4) |
| \[n=\dfrac{n_{o}N}{n_{o}+N-1}\] | (5) | |
| ajsutado | \[IC_{\mu}: \bar{x} \pm t_{\alpha/2} \hspace{.1cm}\frac{s}{\sqrt{n}} \sqrt{\dfrac{N-n}{N-1}}\] | (6) |
| proporción | \[IC_{p}: \widehat{p} \pm z_{\alpha/2} \hspace{.1cm}\sqrt{\frac{\widehat{p}(1-\widehat{p})}{n}}\] | (7) |
| tamaño muestra | \[n=\dfrac{z^{2} p(1-p)}{e^{2}}\] | (8) |
| \[n=\dfrac{Z_{\alpha/2}^{2} \times 0.50(1-0.50)}{e^{2}}\] | (9) | |
| varianza | \[IC_{\sigma^{2}}: \Bigg( \dfrac{(n-1)S^{2}}{\chi^{2}_{\alpha/2}} ;\dfrac{(n-1)S^{2}}{\chi^{2}_{1-\alpha/2}} \Bigg)\] | (10) |
| diferencia medias | \[IC_{d=x_{1}-x_{2}}: \bar{d} \pm t_{\alpha/2} \dfrac{s_{d}}{\sqrt{n}}\] | (11) |
| \[(x_{1}-x_{2})\pm t_{\alpha/2} \hspace{.2cm}s_{p} \sqrt{\frac{1}{n_{1}}+\frac{1}{n_{2}}}\] | (12) | |
| \(s_{p}^{2}\) es \(s_{p}^{2}=\dfrac{(n_{1}-1)s_{1}^{2}+(n_{2}-1)s_{2}^{2}}{n_{1}+n_{2}-2}\) y \(v=n_{1}+n_{2}-2\) | ||
| \[(x_{1}-x_{2})\pm t_{\alpha/2} \sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}\] | (13) | |
| \[v=\frac{(s_{1}^{2}/n_{1}+s_{2}^{2}/n_{2})^{2}}{\Big[(s_{1}^{2}/n_{1})^{2}/(n_{1}-1)\Big]+\Big[(s_{2}^{2}/n_{2})^{2}/(n_{2}-1)\Big]}\] | ||
| diferencia de proporciones | \[IC_{p}: (\widehat{p_{1}} - \widehat{p_{2}}) \pm z_{\alpha/2} \hspace{.1cm}\sqrt{\frac{\widehat{p_{1}}(1-\widehat{p_{1}})}{n_{1}}+ \frac{\widehat{p_{2}}(1-\widehat{p_{2}})}{n_{2}}}\] | (14) |
| razón de varianzas | \[\Bigg(\dfrac{s_{1}^{2}}{s_{2}^{2}} \dfrac{1}{f_{1-\alpha/2}(v_{1},v_{2})}; \dfrac{s_{1}^{2}}{s_{2}^{2}}\dfrac{1}{f_{\alpha/2}(v_{2},v_{1})}\Bigg)\] | (15) |