Variables discretas

En el caso de las variables discretas la función de distribución de probabilidad \(f(x)\) debe cumplir las siguientes propiedades


En este caso se puede utilizar la función sumatoria sum(x, na.rm = FALSE), donde x es un vector y na.rm indica si el vector tienen datos faltantes.



Ejemplo1

Para la función \(f(x)\)

\[f_{_{X}}(x) = \left \{ \begin{matrix} \displaystyle\binom{40}{x}(0.7)^{x}(0.3)^{40-x} & \mbox{si } x=0,1,2,\ldots,40\\ & \\ 0 & \mbox{en otro caso } \end{matrix}\right. \]

  • Construir su representación gráfica
  • Verificar que la suma de todas las probabilidades es igual a uno
  • Calcular \(P(20 \leq X \leq 30)\)
  • Calcular \(E[X]\)
  • Calcular \(V[X]\)



# declaracion de la funcion
fw=function(w){choose(40,w)*0.70^w*0.30^(40-w)}
w=0:40

# grafico de la funcion
plot(w, fw(w), pch=19, col="#BC2B6A", las=1)
grid()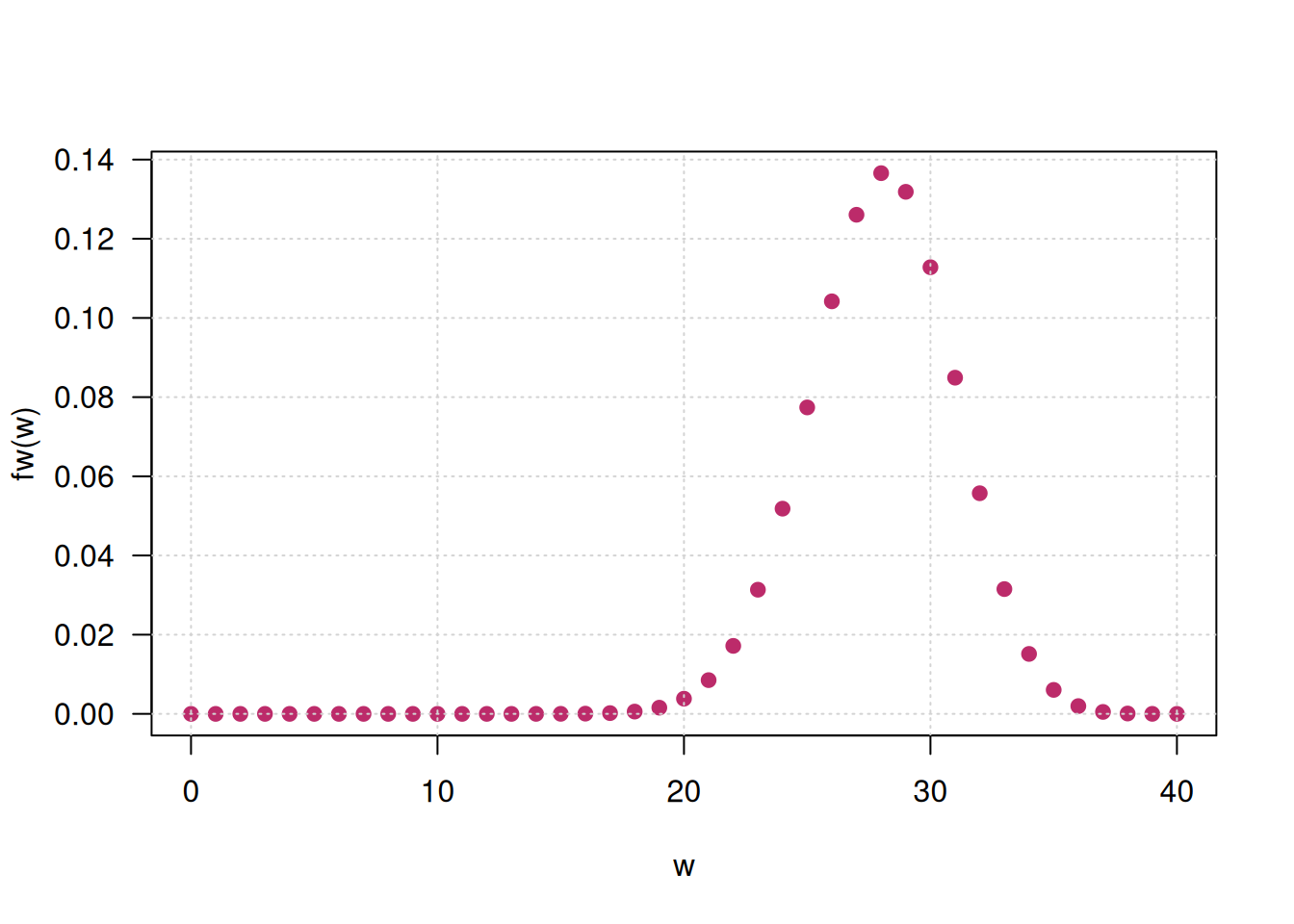



Para verificar que la suma de todas las probabilidades es igual a uno

fw=function(w){choose(40,w)*0.70^w*0.30^(40-w)}
w=0:40
sum(fw(w))
[1] 1



Para calcular la probabilidad \(P(20 \leq X \leq 30)\)

sum(fw(20:30))
[1] 0.8016552




Valor esperado


fw=function(w){choose(40,w)*0.70^w*0.30^(40-w)}
w=0:40
Ex=sum(fw(w)*w)
cat("E[X] = ",Ex)
E[X] =  28




Varianza

fw=function(w){choose(40,w)*0.70^w*0.30^(40-w)}
w=0:40
Ex=sum(fw(w)*w)
Ex2=sum(fw(w)*w^2)
Vx=Ex2-Ex^2
cat("V[X] = ",Vx)
V[X] =  8.4




Variables continuas

Integración

El concepto de integración se utiliza en probabilidad para determinar el área bajo la curva de una función de densidad \(f(x)\) para una variable aleatoria continua.

Dos de las propiedades de una \(f(x)\) son:

  • \(\displaystyle\int\limits_{-\infty}^{+\infty} \dfrac{1}{4} f(x) \:dx = 1\)

  • \(P(a \leq X \leq b) = \displaystyle\int\limits_{a}^{b} f(x) \:dx\)



Estas verificaciones se pueden realizar en R con dos instrucciones:

  • Construcción de la función en R
  • Realizar la integral : para ello utilizamos la función integrate que tiene los parámetros, integrate( f, lower, upper)
    • f: la función
    • lower : limite inferior . Puede ser un número o -Inf
    • upper : limite superior . Puede ser un número o +Inf

integrate(function(x), lower = 0, upper = 1)




Ejemplo 2

Para la función \(f(x)\)

\[f_{_{X}}(x) = \left \{ \begin{matrix} \dfrac{1}{4} e^{-x/4} & \mbox{ , } x \geq 0\\ & \\ 0 & \mbox{en otro caso } \end{matrix}\right. \]

\(P(X < 5)\)$

  • Representar gráficamente la ingral
  • Calcular su valor
  • Calcular para esta variable \(E[X]\)
  • Calcular \(V[X]\)


# declaracion de la funcion
fx=function(x){1/4*exp(-x/4)}

# representación gráfica de la función
x=0:20
plot(x,fx(x), type="l", col="#FFAD42", lwd=5)

# área de integración
x1=seq(0,5,0.01)
f1=fx(x1)
polygon(c(0,x1,5),c(0,f1,0),col="#4983F6")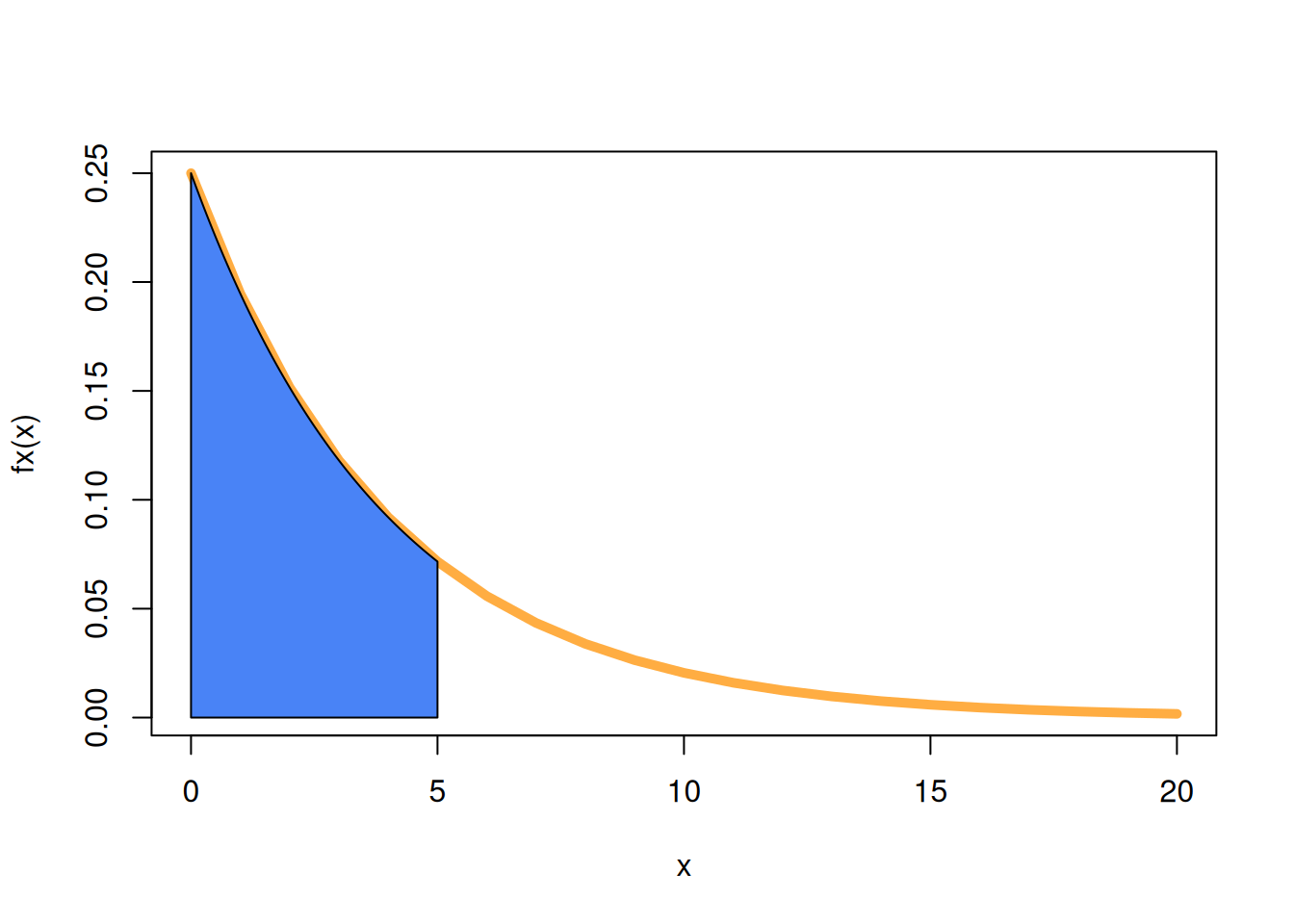



# integral entre 5 y 15 : P( X < 5)
integrate(fx, 0,5)
0.7134952 with absolute error < 7.9e-15




Valor esperado

\[E(X) = \displaystyle\int\limits_{-\infty}^{+\infty}x f(x)dx\]

En este caso la función se multiplica por \(x\)

Mx=function(x){1/4*exp(-x/4)*x}
Ex=integrate(Mx, 0, Inf)
cat("E[X] = ", Ex$value,"\n")
E[X] =  4




Varianza

\[V[X] = E[X^{2}]-(E[X])^{2} = E[X^{2}]-\mu^{2}\]

fx=function(x){1/4*exp(-x/4)}
Mx1=function(x){1/4*exp(-x/4)*x}
Mx2=function(x){1/4*exp(-x/4)*x^2}
Ex=integrate(Mx1, lower=0,upper=Inf)
Ex2=integrate(Mx2, lower=0,upper=Inf)

cat("V[X] = ", Ex2$value-Ex$value^2)
V[X] =  16



fx=function(x){1/4*exp(-x/4)}
Mx1=function(x){1/4*exp(-x/4)*x}
Mx2=function(x){1/4*exp(-x/4)*x^2}
Ex=integrate(Mx1, lower=0,upper=Inf)
Ex2=integrate(Mx2, lower=0,upper=Inf)
cat("E[X] = ", Ex$value,"\n")
E[X] =  4 
cat("V[X] = ", Ex2$value-Ex$value^2)
V[X] =  16



Otras herramientas


Symlab

https://es.symbolab.com/



Nota

El hecho que nos apoyemos en herramientas como WolframAlpha, Symlab, ChatGPT, no implica que no seamos capaces de desarrollar procesos simples de integración. Estas herramientas deben ser utilizadas como medio de comprobación de los resultados obtenidos en el desarrollo de los problemas planteados.