Problema 1

Clasifique las siguientes variables como discretas o continuas:

X : el número de accidentes automovilísticos que ocurren durante un dia en Cali
Y : tiempo que se tarda una persona en recorrer 100 metros en segundos
M : cantidad de leche que una vaca produce semanalmente en litros
Z : el número de huevos que una gallina produce semanalmente
G : número de permisos para la construcción que son aprobados mensualmente en Cali
Q : peso en kilogramos de automóvil
R : embergadura de las alas de un condor en edad adulta en metros
S : tiempo que dedica una persona al ocio - tiempo no productivo en horas
T : ingresos de una familia en pesos por mes
V : cantidad de calorias que contiene una bebida gaseosa
W : largo del femur de un adulto humano en centimetros




Problema 2

Determine el valor de \(C\) de modo que cada una de las siguientes funciones sirva como una función de probabilidad de una variable aleatoria discreta

\[f(x) = C \binom{2}{x} \binom{3}{3-x}, \text{ para } x=0,1,2\]




Problema 3

Un embarque de 7 televisores contiene 2 unidades defectuosas. Un hotel compra al azar 3 de los televisores. Si \(X\) es el número de unidades defectuosas en un grupo de tres televisores comprados por el hotel al azar, encuentra la función de probabilidad de \(X\). Expresa los resultados de forma gráfica. Construye la función de distribución acumulada de \(X\). Usar \(F(X)\) para responder, ¿cuál es la probabilidad que hayan cero televisores defectuosos en el grupo de tres televisores?, ¿cuál es la probabilidad que haya más de 1 televisor defectuoso en la selección de tres televisores?.




Problema 4

La distribución de probabilidad de \(X\), el número de imperfecciones por 10 metros de una tela sintética en rollos continuos de ancho uniforme, está dada por

\(x\) 0 1 2 3 4
\(f(x)\) 0.41 0.37 0.16 0.05 0.01




Problema 5

Sea \(W\) el número de sellos en tres lanzamientos de una moneda. Liste los elementos del espacio muestral \(S\) para los tres lanzamientos de la moneda y asigne un valor \(w\) de \(W\) a cada punto muestral.




Problema 6

Encuentre la distribución de probabilidad de la variable aleatoria W del ejercicio anterior; suponga que la cara está cargada de manera que una cara tenga doble de probabilidad de ocurrir que un sello.




Problema 7

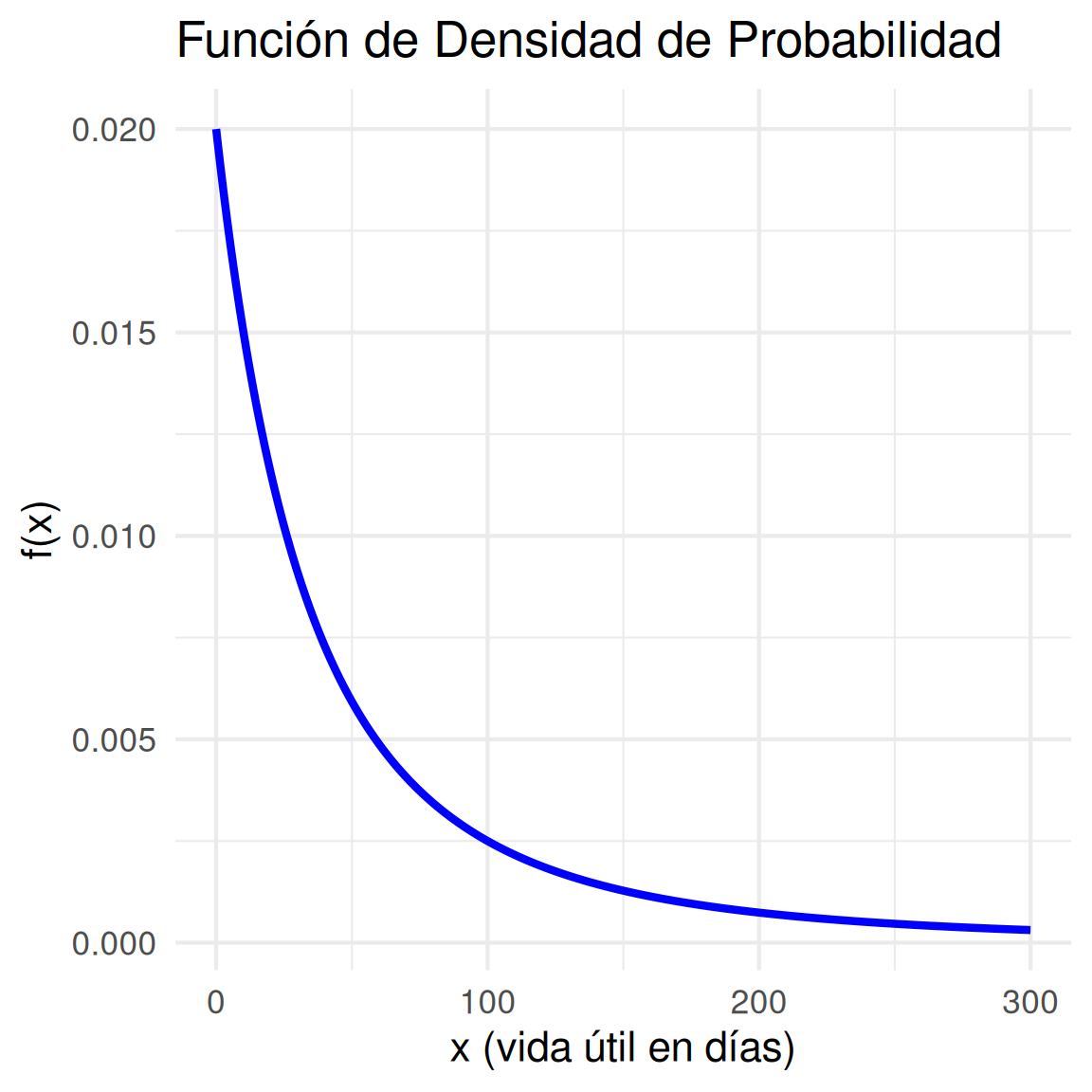
La vida útil en días, para frascos de cierta medicina de prescripción es una variable aleatoria que tiene función de densidad,

\[f_{_{X}}(x) = \left \{ \begin{matrix} \dfrac{20000}{(x+100)^{3}}, & \mbox{ } x \geq 0\\ & \\ 0 , & \mbox{en cualquier otro caso } \end{matrix}\right. \]

Encuentre la probabilidad de que un frasco de esta medicina tenga una vida útil de :




Problema 8

El número total de horas, medidas en unidades de 100 horas, que una familia utiliza una lavadora en un periodo de un año es una variable aleatoria continua \(X\) que tiene la función de densidad,

\[f_{_{X}}(x) = \left \{ \begin{matrix} x ,& \mbox{ } 0 \leq x < 1\\ & \\ 2-x ,& \mbox{ } 1 \leq x \leq 2\\ &\\ 0 ,& \mbox{en cualquier otro caso } \end{matrix}\right. \]

Encontrar la probabilidad de :




Problema 9

Una variable aleatoria continua \(X\) que puede tomar valores entre \(x = 1\) y \(x = 3\) tiene una función de densidad dada por \(f (x) = 1/2\).

Para la función de densidad del ejercicio anterior encuentre \(F(x)\). Utilíce la función obtenida para encontrar:




Problema 10

En una tarea de laboratorio, cuando el equipo está operando la función de densidad del resultado, \(X\), es el tiempo,

\[f_{_{X}}(x) = \left \{ \begin{matrix} 2(1-x), & \mbox{ } 0 \leq x \leq 1\\ & \\ 0 , & \mbox{en cualquier otro caso } \end{matrix}\right. \]




Problema 11

La probabilidad de tener una unidad defectuosa en una línea de ensamblaje es de \(p = 0.05\). Si el conjunto de unidades terminadas constituye un conjunto de ensayos independientes, la función de probabilidad de número de unidades defectuosas está dada por,

\[f(x) = \binom{10}{x} p^{x} (1 − p)^{10−x} \text{, } x = 0, 1, . . . , 10\]




Problema 12

El gerente de un restaurante que sólo da servicio mediante reservas sabe, por experiencia, que el \(20\)% de las personas que reservan una mesa no asistirán. Si el restaurante acepta \(25\) reservas pero sólo dispone de \(20\) mesas, ¿cuál es la probabilidad de que a todas las personas que asistan al restaurante se les asigne una mesa?.


La función de probabilidad del número de personas que llegan al restaurante es,

\[f(x) = \binom{25}{x} (0.80)^{x} (0.20)^{25−x} \text{, } x = 0, 1, . . . , 25\]




Nota

En todos los casos represente gráficamente la función de probabilidad correspondiente y en ella resalte las probabilidades solicitadas.




AYUDAS

\[\sum_{x=0}^{2} \binom{2}{x} \binom{3}{3-x} \]

x=0:2
sum(choose(2,x)*choose(3,3-x))

x=0:2
sum(choose(2,x)*choose(3,3-x))




\[\int_{0}^{\infty} \dfrac{20000}{(x+100)^{3}} \,dx\]

# Definir la función 
fx7 <- function(x) {
  20000 / (x + 100)^3
}
# Calcular la integral definida desde 0 hasta infinito
result <- integrate(fx7, lower = 0, upper = Inf)

# Imprimir el resultado
result



Show in New Window
1 with absolute error < 4.7e-07

# Definir la función 
fx7 <- function(x) {
  20000 / (x + 100)^3
}
# Calcular la integral definida desde 0 hasta infinito
result <- integrate(fx7, lower = 0, upper = Inf)

# Imprimir el resultado
result
## 1 with absolute error < 4.7e-07
# Cargar librería
library(ggplot2)

# Definir la función de densidad
f_x <- function(x) {
  ifelse(x >= 0, 20000 / (x + 100)^3, 0)
}

# Crear una secuencia de valores de x
x_vals <- seq(0, 300, length.out = 1000)

# Evaluar la función en los valores de x
y_vals <- sapply(x_vals, f_x)

# Crear un data frame para graficar
df <- data.frame(x = x_vals, y = y_vals)

# Graficar la función de densidad
ggplot(df, aes(x, y)) +
  geom_line(color = "blue", size = 1) +
  labs(title = "Función de Densidad de Probabilidad",
       x = "x (vida útil en días)",
       y = "f(x)") +
  theme_minimal()