¿Que es un indicador?

Cuando nos subimos a un auto observamos un tablero con muchos indicadores que permiten al conductor validar el estado del vehículo. Todos los podemos visualizar al tiempo con el fin de darnos una idea del nivel de combustible, la temperatura, el estado de la batería, si alguna puerta esta abierta, la velocidad a la que se viaja, entre otros.

Al igual que la situación anterior cuando nos enfrentamos a una análisis de datos, requerimos resumirlos en indicadores, tablas y gráficos que nos permitan un fácil análisis de ellos

Tomaremos una base de datos de la FIFA para analizar indicadores de las selecciones de futbol asociadas a 6 confederaciones.

library(DT)
DT::datatable(head(futbol, 218),fillContainer = FALSE, options = list(pageLength = 8))

# DT::datatable(head(Visitantes, 389455),fillContainer = FALSE, options = list(pageLength = 8))

portal FiveThirtyEight : https://data.fivethirtyeight.com/

Tablas de frecuencia

Tablas de frecuencia para variables cualitativas

Las distribuciones de frecuencia o también llamadas tablas de frecuencia nos sirven para agrupar los datos y así permitir resumir para poder tener una idea mas clara de sus características.

Para las variables cualitativas la tabla posee 3 columnas :

c1: los diferentes valores que toma la variable.
c2: frecuencia absoluta que consiste en el conteo para cada uno de los valores distintos que toma la variable.
c3: frecuencia relativa que corresponde al porcentaje la cantidad de datos para cada los valores

# Forma simple
# tabla1 <- table(Visitantes$Mes)
# names(tabla1) <- c("Ene", "Feb", "Mar", "Abr", "May", "Jun", "Jul", "Ago", "Sep", "Oct", "Nov", "Dic")
# tabla1

# Forma simple
table(futbol$confed)


     AFC      CAF CONCACAF CONMEBOL      OFC     UEFA 
      46       55       41       10       10       56

#utilizando summarytools
# Pais=as.factor(Visitantes$`País de Residencia`)
# summarytools::freq(Pais, cumul = FALSE)
#utilizando summarytools
confederacion=as.factor(futbol$confed)
summarytools::freq(confederacion, cumul = FALSE)

Error in match.call(f, call): ... used in a situation where it does not exist

Frequencies  

                 Freq   % Valid   % Total
-------------- ------ --------- ---------
           AFC     46     21.10     21.10
           CAF     55     25.23     25.23
      CONCACAF     41     18.81     18.81
      CONMEBOL     10      4.59      4.59
           OFC     10      4.59      4.59
          UEFA     56     25.69     25.69
          <NA>      0                0.00
         Total    218    100.00    100.00

Nota: paquete summarytools

Tablas de frecuencia para variables cuantitativas

Para las variables cuantitativas las tablas de frecuencias tiene una presentación diferente a la vista anteriormente. Como se trata de variables con una gran número de valores diferentes, es necesario dividirlas por intervalos .

Cuando tenemos los datos sin agrupar nos es difícil extraer información que nos permita hacer un análisis de los mismos

nf=c(4.1, 2.7, 3.1, 3.2, 3.0, 3.2, 2.0, 2.4, 1.6, 3.2, 3.1, 2.6, 2.0, 2.4, 2.8, 3.3, 4.0, 3.4, 3.0, 3.1, 2.7, 2.7, 3.0, 3.8, 3.2, 2.2, 3.5, 3.5, 3.8, 3.5, 3.9, 4.2, 4.3, 3.9, 3.2, 3.5, 3.5, 3.7, 4.1, 3.7, 3.5, 3.6, 3.2, 3.1, 3.4, 3.0, 3.0, 3.0, 2.7, 1.7, 3.6, 2.1, 2.4, 3.0, 3.1, 2.5, 2.5, 3.6, 2.2, 2.4, 3.1, 3.3, 2.7, 3.7, 3.0, 2.7, 3.0, 3.2, 3.1, 2.4, 3.0, 2.7, 2.5, 3.0, 3.0, 3.0, 3.2, 3.1, 3.8, 4.1, 3.7, 3.5, 3.0, 3.7, 3.7, 4.1, 3.7, 3.9, 3.7, 2.0)
nf

 [1] 4.1 2.7 3.1 3.2 3.0 3.2 2.0 2.4 1.6 3.2 3.1 2.6 2.0 2.4 2.8 3.3 4.0 3.4 3.0
[20] 3.1 2.7 2.7 3.0 3.8 3.2 2.2 3.5 3.5 3.8 3.5 3.9 4.2 4.3 3.9 3.2 3.5 3.5 3.7
[39] 4.1 3.7 3.5 3.6 3.2 3.1 3.4 3.0 3.0 3.0 2.7 1.7 3.6 2.1 2.4 3.0 3.1 2.5 2.5
[58] 3.6 2.2 2.4 3.1 3.3 2.7 3.7 3.0 2.7 3.0 3.2 3.1 2.4 3.0 2.7 2.5 3.0 3.0 3.0
[77] 3.2 3.1 3.8 4.1 3.7 3.5 3.0 3.7 3.7 4.1 3.7 3.9 3.7 2.0

Una primera aproximación pude ser el diagrama de tallos y hojas con consiste en separar los dígitos de los datos en dos : una primera parte que se repite llamada tallo y otra parte que tiene diversos valores. Este diagrama también nos permite ordenar los datos de menor a mayor

stem(nf)


  The decimal point is at the |

  1 | 67
  2 | 00012244444
  2 | 555677777778
  3 | 0000000000000011111111222222223344
  3 | 555555566677777777888999
  4 | 0111123

Una forma de construir una tabla de freciencias por intervalos es utilizando la funcion graph.freq del paquete agricolae

library(agricolae)
h2=with(futbol,graph.freq(off,plot=FALSE))
t2=table.freq(h2)
colnames(t2) = c("  LI  ", "  LS  ", "marca clase'", "Frec.Abs","Frec.Rel", "Frec.Abs.Ac","Frec.Rel.Ac")
t2

    LI     LS   marca clase' Frec.Abs Frec.Rel Frec.Abs.Ac Frec.Rel.Ac
1   0.20   0.58         0.39       40     18.3          40        18.3
2   0.58   0.96         0.77       52     23.9          92        42.2
3   0.96   1.34         1.15       53     24.3         145        66.5
4   1.34   1.72         1.53       32     14.7         177        81.2
5   1.72   2.10         1.91       21      9.6         198        90.8
6   2.10   2.48         2.29        9      4.1         207        95.0
7   2.48   2.86         2.67        6      2.8         213        97.7
8   2.86   3.24         3.05        4      1.8         217        99.5
9   3.24   3.62         3.43        1      0.5         218       100.0

Frec.Abs : Frecuencia absoluta
Frec.Rel : Frecuencia relativa

Frec.Abs.Ac : Frecuencia Absoluta Acumuada
Frec.Rel.Ac : Frecuencia Relativa Acumulada

Si se requiere dividir el rango en intervalos determinados se utiliza la función cut

c <- cut(futbol$off, breaks = c(0, 0.999, 1.99, 2.99, 3.995, 4))
levels(c) <- c("[0-1)", "[1-2)", "[2-3)", "[3-4)","[4-5]")
table(c)

c
[0-1) [1-2) [2-3) [3-4) [4-5] 
   95    99    21     3     0

data("iris")
summarytools::freq(iris$Species, cumul = FALSE, headings = FALSE)

Error in match.call(f, call): ... used in a situation where it does not exist


                   Freq   % Valid   % Total
---------------- ------ --------- ---------
          setosa     50     33.33     33.33
      versicolor     50     33.33     33.33
       virginica     50     33.33     33.33
            <NA>      0                0.00
           Total    150    100.00    100.00

Rango percentil

Es un número que divide la muestra en dos partes. $x$ % de los datos de la muestra son iguales o menores que $P_{x}$ y un $(100-x)$ % por encima de el.

Para ilustrar el concepto, pensemos en que participamos de una carrera y que el grupo está conformado por 100 corredores. El percentil dará cuenta de mi posición dentro del grupo. Por ejemplo si mi posición en la carrera en orden de llegada es la décima, indica que por detrás de mi están 90 atletas. Indica esto que soy el percentil 90 ($P_{90}$).

Reto :

Que significado tiene :

Participar en una carrera K10 y ocupar el percentil 30 : $P_{30}$
Una nota en un examen de matemáticas ocupó el percentil 90 : $P_{90}$
Que significa: $P_{25}$ ; $P_{50}$ ; $P_{75}$

Diagrama de cajas

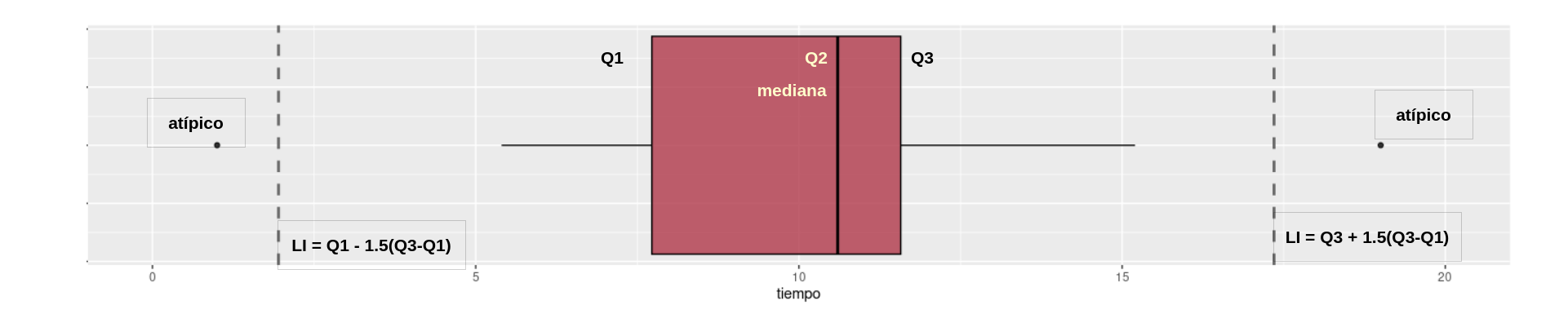
# p=ggplot(futbol, aes(x=off))+geom_boxplot(fill = "#b0394a",           # Color caja
#                alpha = 0.3,        # Transparencia
#                color = "#000000",          # Color del borde
#                outlier.colour = "#000000") # Color atípicos
# 
# p + geom_text(data = NULL, x = 1.5, y = 0.4, label = "Q3",col="#b0394a")+
#     geom_text(data = NULL, x = 1.03, y = 0.4, label = "Q2 = mediana",col="#b0394a")+
#     geom_text(data = NULL, x = 0.65, y = 0.4, label = "Q1",col="#b0394a") +
#     geom_text(data = NULL, x = 0.2, y = 0.4, label = "mín",col="#b0394a") +
#     geom_text(data = NULL, x = 3.5, y = 0.4, label = "máx",col="#b0394a") +
#     geom_text(data = NULL, x = 3, y = 0.4, label = "atípicos",col="#b0394a") +
#     geom_text(data = NULL, x = 1.166468, y = 0, label = "*  media",col="#b0394a")# +
#  #   geom_text(data = NULL, x = 1.2, y = 0.4, label = "media",col="#b0394a")

atípico | $LI=Q_{1}- 1.5(Q_{3}-Q_{1})$ | $Q_{1}$ | $Q_{2}$ | $Q_{3}$ | $LS=Q_{3}+ 1.5(Q_{3}-Q_{1})$ | atípico

Con ayuda del diagrama de tallos y hojas es posible ubicar los percentiles en un conjunto de datos

stem(futbol$off)


  The decimal point is 1 digit(s) to the left of the |

   2 | 00000011112345688345788
   4 | 01125991123445567
   6 | 0022444456788899900012333666789999
   8 | 112455677888900234668
  10 | 00113344555567889912233456899
  12 | 001344566677890002223456789
  14 | 0667789012344566678
  16 | 012355724578
  18 | 026788922679
  20 | 34481278
  22 | 2446
  24 | 2224
  26 | 900
  28 | 06
  30 | 44
  32 | 
  34 | 4

En este caso el valor mínimo corresponde a 0.20 y el máximo a 3.44

Ahora determine en este diagrama los percentiles :

$P_{25}$
$P_{50}$
$P_{75}$
$P_{10}$

Es más rápido utilizando la función de R : quantile

quantile(futbol$off, c(0.25,.50,0.75,0.10))

  25%   50%   75%   10% 
0.690 1.075 1.540 0.380

Renumen

Percentiles	Divide la muestra en 100 partes de igual porcentaje, cada una con un 1%. $P_{1}, P_{2}, \dots P_{99}$
Deciles	Dividen la muestra en 10 parte de igual porcentaje, cada una con un 10%. $D_{1}, D_{2}, \dots D_{9}$
Quintiles	Dividen la muestra en 5 partes de igual porcentaje, cada una con un 20%. $K_{1}, K_{2}, K_{3}, K_{4}$
Cuartiles	Dividen la muestra en 4 partes de igual porcentaje, cada una con un 25%. $Q_{1}, Q_{2}, Q_{3}$

Indicadores de los Datos

Central	Dispersión	Forma
media	rango	sesgo o asimetría
mediana	varianza	curtosis
moda	desviación estándar
media truncada	coeficiente de variación
rango medio
media armónica
media geométrica
media ponderada

Indicadores de Centro

Media aritmética

\[\bar{x}= \frac{1}{n} \sum_{i=1}^{n} x_{i}\]

Es una de los indicadores estadísticos mas conocidos

Propiedades de la media :

La suma de las desviaciones de los datos con respecto a la media es cero. $\sum (x_{i}-\bar{x})=0$.
La suma de los cuadrados de las desviaciones de los datos con respecto a un valor $a$ es mínimo cuando $a=\bar{x}$.
Si $x_{i}=k$ para todo $i$, entonces, $\bar{x}=k$.
Si a todos los datos de una variable se le suma una constante $k$, es decir $y_{i}=x_{i} + k$, entonces $\bar{y}=\bar{x} +k$
Si todos los datos de una variable se multiplican por una constante $k$, es decir $y_{i}=kx_{i}$, entonces $\bar{y}=k\bar{x}$
Si $z_{i}=a x_{i}+b y_{i}$, donde: a, b constantes y $x_{i}$, $y_{i}$ variables, entonces: $\bar{z}=a\bar{x}+b\bar{y}$.

Ejemplo 1

El promedio de el rendimiento de millas por galón de combustible del grupo de autos observados es de $20.09$ mpg

mean(mtcars$mpg,na.rm = TRUE)

[1] 20.09062

Ejemplo 2

El valor promedio de poder ofencivo de las selecciones de futbol asociadas a la FIFA es de 1.16

mean(futbol$off, na.rm = TRUE)

[1] 1.166468

Ejemplo 3

El promedio del conjunto de números enteros entre uno y diez es 5.5

x=1:10
x

 [1]  1  2  3  4  5  6  7  8  9 10

cat("media :",mean(x))

media : 5.5

Ejemplo 4

Surge el problema a que se puede tener es este indicador cuando uno de sus datos cambia drásticamente, por ejemplo si se cambia el último datos (10) por otro valor como 100 entonces, que pasaría con la media ?

En este caso el promedio se eleva a 14.5 por el cambio realizado. Esto puede suceder en algunos casos donde trabajamos información que puede presentar datos extremos o atípicos

x=1:10
x[10]=100
x

 [1]   1   2   3   4   5   6   7   8   9 100

cat("media :" ,mean(x))

media : 14.5

La media se emplea cuando los datos son simétricos y no se poseen datos atípicos.

Mediana

Me :Es el número que divide la muestra en dos partes de igual proporción (50% : 50%). Es decir que corresponde a:

\[P_{50} = D_{5} = Q_{2}\]

también corresponde a la linea central del diagrama de cajas.

median(futbol$off,na.rm = TRUE)

[1] 1.075

boxplot(futbol$off, las=1, horizontal = TRUE, col = c1)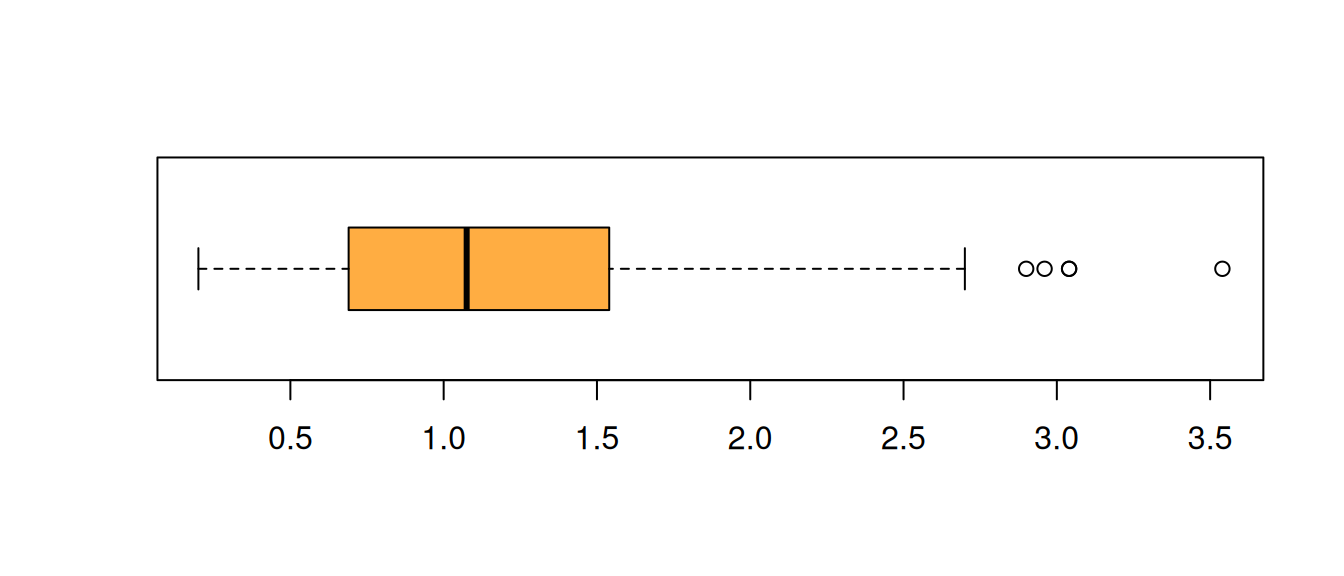

La Me corresponde a la linea central de a caja en el diagrama de cajas

La mediana es mas robusta a los cambio en los datos extremos. En presencia de datos atípicos es mejor utilizar la mediana en lugar que la media.

x=1:10
x

 [1]  1  2  3  4  5  6  7  8  9 10

cat("media :" ,median(x))

media : 5.5

x[10]=20
x

 [1]  1  2  3  4  5  6  7  8  9 20

cat("media :" ,median(x))

media : 5.5

Moda

Mo : Dato o valor que más se repite. Es utilizada como medida de tendencia central en variables cualitativas o o en cuantitativas discretas con pocos valores. En una tabla o gráfico se puede distinguir fácilmente.

#utilizando summarytools
summarytools::freq(futbol$confed, cumul = FALSE, headings = FALSE)

Error in match.call(f, call): ... used in a situation where it does not exist


                 Freq   % Valid   % Total
-------------- ------ --------- ---------
           AFC     46     21.10     21.10
           CAF     55     25.23     25.23
      CONCACAF     41     18.81     18.81
      CONMEBOL     10      4.59      4.59
           OFC     10      4.59      4.59
          UEFA     56     25.69     25.69
          <NA>      0                0.00
         Total    218    100.00    100.00

moda : UEFA, es la confederación con más selecciones nacionales de futbol ascritas

Otras medidas de centro

Media truncada

Con el fin de evitar que los datos atípicos generen sesgos en el indicador de la media, es posible separar el 90% de los datos, quitando un 5% de los datos mas pequeños y un 5% de los datos mayores. A este indicador de le llama media truncada al 10% ($\bar{x}_{_{0.10}}$)

mean(futbol$off, na.rm = TRUE, trim = 0.10)

[1] 1.111989

Rango medio

\[\frac{1}{2}\big(max(x)+min(x)\big)\]

(max(futbol$off,na.rm = TRUE)+min(futbol$off,na.rm = TRUE))/2

[1] 1.87

La diferencia entre el equipo con mas poder ofencivo y el equipo como menor valor es de 1.87 puntos.

Media geométrica

Este indicador de tendencia central se utiliza para promediar tasa de crecimiento o de interés. Para encontrar su valor se multiplican los valores de $n$ tasas incrementadas en uno ($1+r$). A ese producto se le extrae la raíz n-esima.

\[MG = \Bigg(\displaystyle\prod_{i=1}^n (r_{i}+1)\Bigg)^{1/n}\]

Media armónica

\[H = \dfrac{n}{\frac{1}{x_{1}}+\frac{1}{x_{2}}+ ... + \frac{1}{x_{n}}} \]

Este indicador corresponde al inverso de la media aritmética

Problema reconocimiento de grupo

Spongaos que solo se nos dice que un grupo conformado por 4 personas tiene un promedio de edad de $20$ años. Todos inicialmente suponemos que se trata de cuatro jóvenes que tienen edades cercanas a $20$ años. Pero puede ocurrir que estemos lejos de acertarlo, pues existen multiples combinaciones de edades que tienen como promedio $20$ años.

Por ello es necesario tener más informacion sobre el grupo.

Grupo 1	Grupo 2
Edades : 19, 22, 18, 21	Edades : 39, 38, 2, 1
Promedio : 20 años	Promedio : 20 años

Hace falta otro indicador que nos oriente de cual grupo hablamos cuando solo tenemos como información : media = $20$ años. Esta necesidad la suplen los indicadores de dispersión.

Indicadores de Dispersión

Rango

$r = max(x) - min(x)$

En caso de los dos grupos:

Grupo 1	Grupo 1
$\bar{x} = 20$ años	$\bar{x} = 20$ años
$r = 4$ años	$r = 38$ años

Es importante hacer notar que si además de la media conocemos tambien un indicador de dispersión, en este caso el rango, podemos intuir si se trata del primero o segundo grupo. El ranto es un indicador muy útil cuando se deben realizar cálculos rápidos.

Varianza

Es la medida de dispersión más utilizada en estadística y está definida por

\[s^{2}=\frac{1}{n-1} \sum_{i=1}^{n} (x_{i}-\bar{x})^{2}\]

Propiedades de la varianza

$s^{2} = \frac{1}{n} \sum x_{i}^{2}- (\bar{x})^{2}$
La varianza es siempre no negativa $s^{2} >=0$
La varianza de una constante es cero $s_{k}^{2}=0$
Si $y_{i}= x_{i} + k$, entonces $s_{y}^{2}= s_{x}^{2}$
Si $y_{i}=k x_{i}$, entonces $s_{y}^{2}= k^{2} s_{x}^{2}$
Si $y_{i}=x_{i} + k$ , entonces $s_{y}^{2} = s_{x}^{2}$
Si $z_{i} = a x_{i} + b y_{i}$, entonces $s_{z}^{2}$ = $a^{2}s_{x}^{2}$ + $b^{2}s_{y}^{2}$ + $2ab$ $cov(xy)$

La varianza se puede interpretar como el promedio de las diferencias cuadradas entre cada uno de los datos y la media

El problema de la varianza es su interpretación

Sus unidades son al cuadrado y en la mayoría de los casos no es posible interpretarlos. Por esta razón se optó por utilizar otra mediada de dispersión

Desviación estándar

Es la raíz cuadrada de la varianza

\[s=\sqrt{s^{2}}\]

Nota : no aplican todas las propiedades de la varianza

cat( "Varianza            :",var(futbol$off), "\n" )

Varianza            : 0.4319888

cat("Desviación estándar :",sd(futbol$off))

Desviación estándar : 0.6572586

Aunque la desviación estándar reduce el problema debido a tener las mismas unidades de la variable, es útil para comparación de dos grupos

Coeficiente de variación

Nos indica que tan grande o que tan pequeña es la desviación estándar con respecto a su media

\[CV= \dfrac{s}{\bar{x}} \times 100 \% \]

Existen diferentes reglas empíricas para la interpretación del coeficiente de variación. Una de ellas establece como límite el 20% para separar los grupos homogéneos de los heterogéneos Por lo general se utiliza un valor hasta el 20% para determinar que un grupo de datos son homogéneos, de lo contrario se calificará como heterogéneo.

cat("Coeficiente de variación :",sd(futbol$off)/mean(futbol$off)*100, " %")

Coeficiente de variación : 56.34605  %

En este caso se obtiene un valor muy alto del coeficiente de variación lo cual indica que los datos en este caso el poder ofencivo de los equipos es alta, pudiendo calificar esta variable como heterogenea

Indicadores de Forma

Curtosis

Se mide a través del coeficiente de curtosis que mide cuan puntiaguda es una distribución respecto a la curva de la distribución normal entandar.

De acuerdo con su valor, la puntudez de los datos puede clasificarse en tres grupos:

Leptocúrtica, con valores grandes para el coeficiente ( CA>0)
Mesocúrtica, con valores medianos para el coeficiente ( CA=0)
Platicútrica, con valores pequeños para el coeficiente ( CA<0)

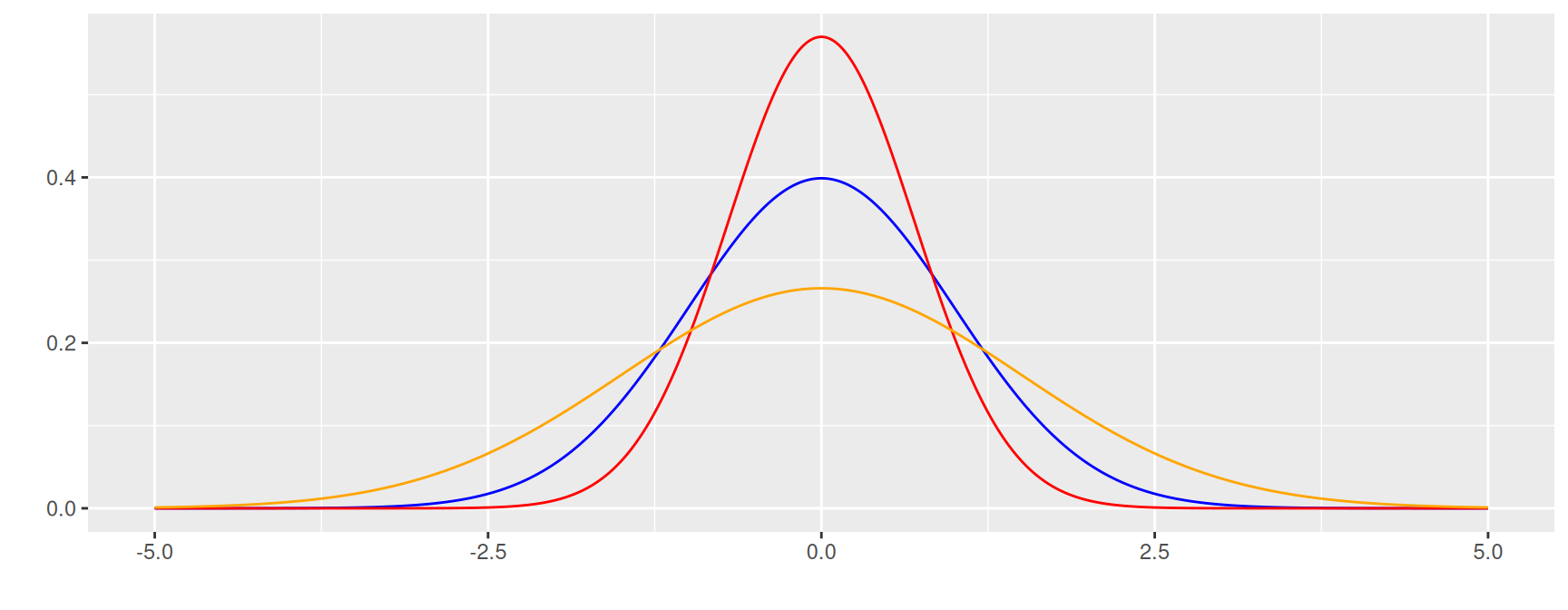
\[CA = \dfrac{1}{s^{4}}\Bigg(\dfrac{1}{n} \sum_{i=1}^{n} (x-\bar{x})^{4} \Bigg) - 3\]

rapportools::kurtosis(futbol$off)

[1] 0.5363538

Asimetría o sesgo

Mide que tanto la forma de la distribución de frecuencias de los datos es simétrica o no con respecto a la media. Esta característica de los datos se mide a través del coeficiente de asimetría o sesgo.

Es simétrica si el valor del indicador es 0 ($\bar{x}=Me$)
Es asimétrica a la izquierda si el valor del indicador es negativo ($\bar{x}<Me$)
Es asimétrica a la derecha si el valor del indicador es positivo ($\bar{x}>Me$)

Asimetria negativa : Poco con poco, mucho con mucho
Simetrica : Poco con poco, poco con mucho, mucho al rededor de un centro
Asimetria positiva : Mucho con poco, poco con mucho

\[CA = \dfrac{1}{s^{4}}\Bigg(\dfrac{1}{n} \sum_{i=1}^{n} (x-\bar{x})^{4} \Bigg) - 3\]

rapportools::skewness(futbol$off)

[1] 0.8169614

El valor obtenido para el sesgos nos indica que existe un mediano sesgo positivo o a la derecha ( mucho con poco - poco con mucho). Este resultado nos indica que muchos equipos tienen bajo nivel ofencivo y unos pocos son los que tienen un alto poder ofencivo.

summarytools::descr(futbol$off)

Error in match.call(f, call): ... used in a situation where it does not exist

Descriptive Statistics  

                    futbol$off
----------------- ------------
             Mean         1.17
          Std.Dev         0.66
              Min         0.20
               Q1         0.69
           Median         1.08
               Q3         1.54
              Max         3.54
              MAD         0.62
              IQR         0.85
               CV         0.56
         Skewness         0.82
      SE.Skewness         0.16
         Kurtosis         0.54
          N.Valid       218.00
                N       218.00
        Pct.Valid       100.00

summarytools::descr(mtcars$mpg)

Error in match.call(f, call): ... used in a situation where it does not exist

Descriptive Statistics  

                    mtcars$mpg
----------------- ------------
             Mean        20.09
          Std.Dev         6.03
              Min        10.40
               Q1        15.35
           Median        19.20
               Q3        22.80
              Max        33.90
              MAD         5.41
              IQR         7.38
               CV         0.30
         Skewness         0.61
      SE.Skewness         0.41
         Kurtosis        -0.37
          N.Valid        32.00
                N        32.00
        Pct.Valid       100.00

d1=density(futbol$off, na.rm=TRUE); plot(d1)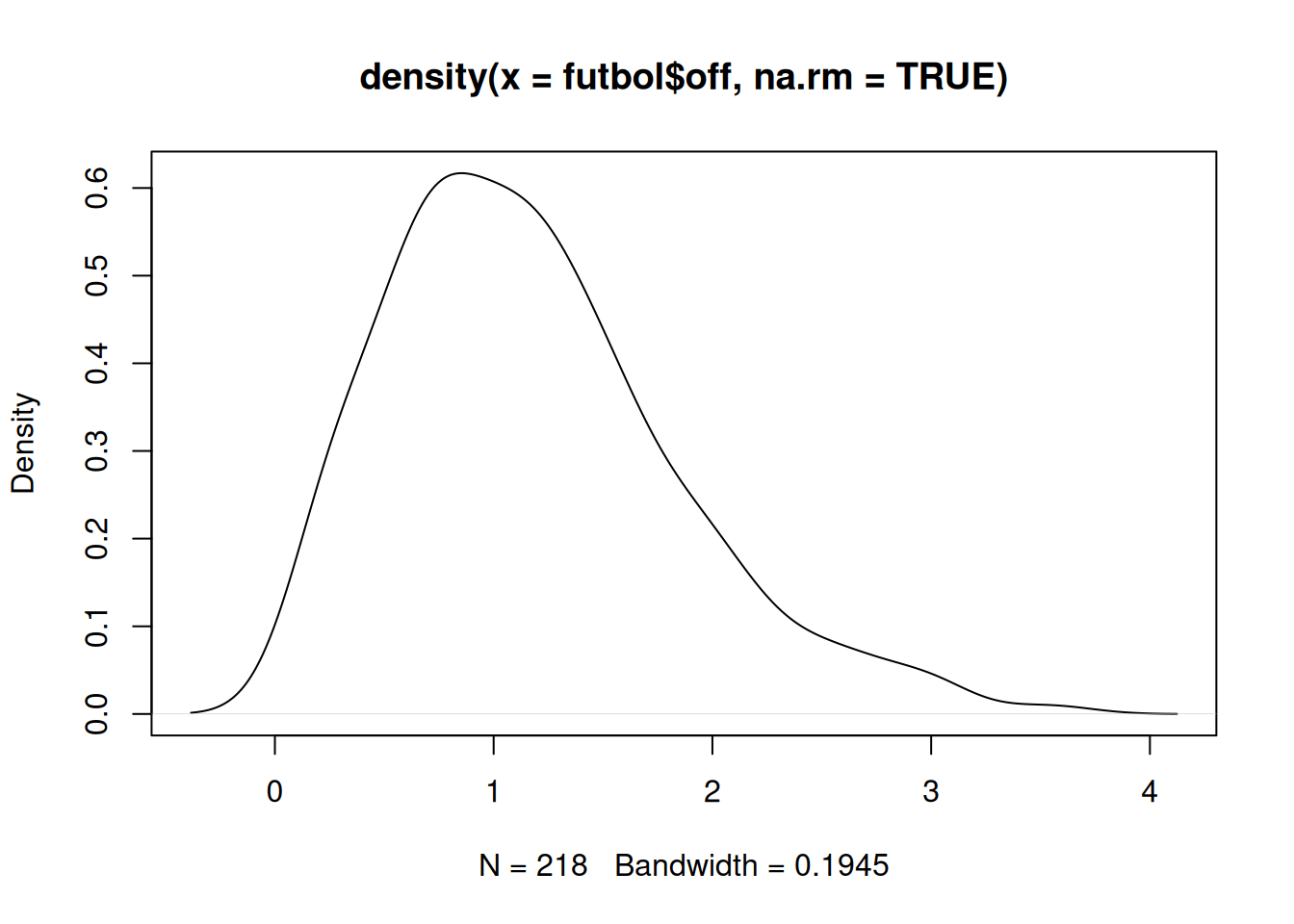

data("mtcars")
d2=density(mtcars$mpg); plot(d2)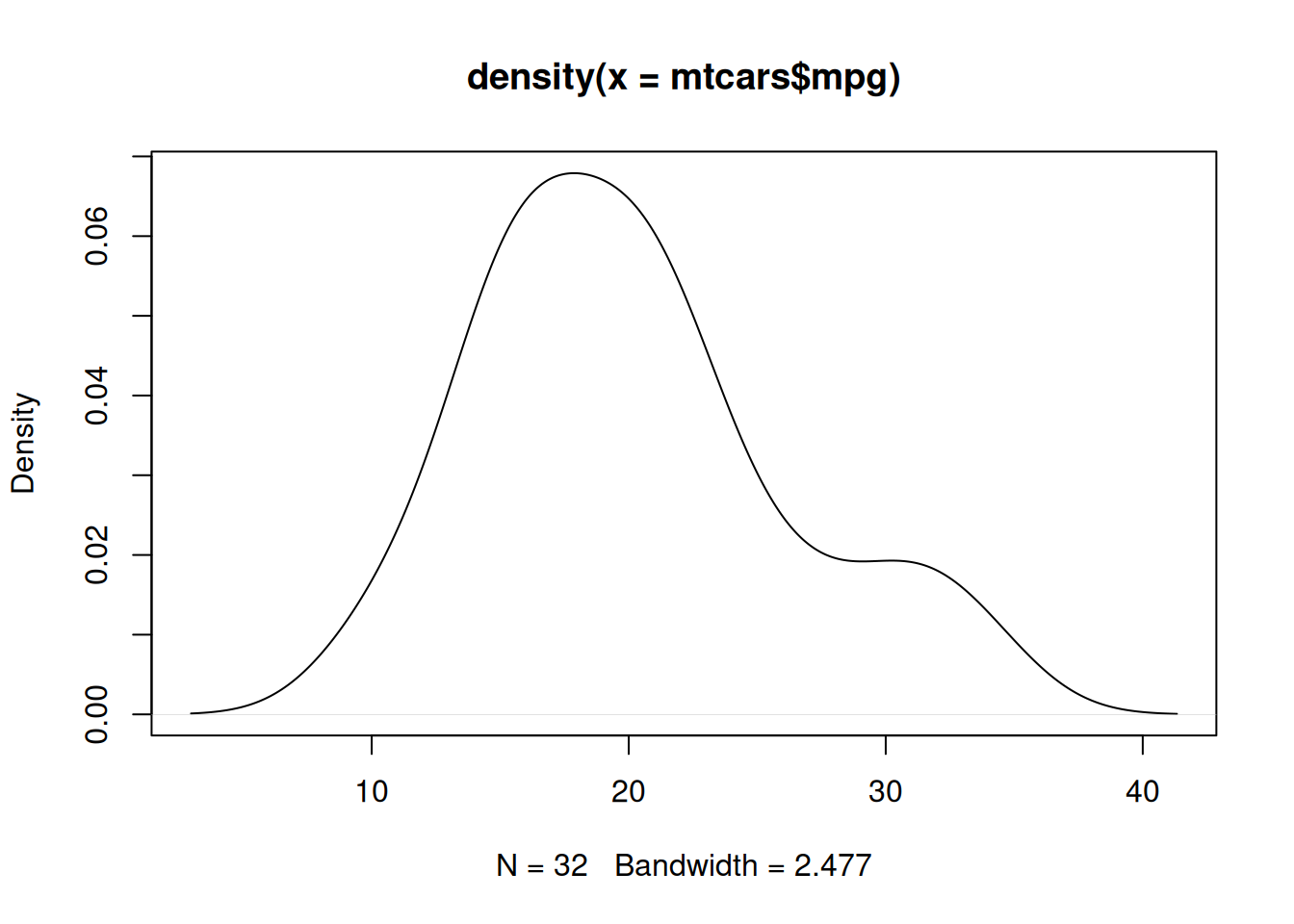

Formulario

Estadística	fórmula	código R
centro
media aritmética	$\displaystyle\dfrac{1}{n}\sum_{i=1}^{n} x_{i}$	`mean(x)`
mediana	$Me = P_{50} = X_{n+1/2}$	`median(x)`
moda	$Mo$ dato que más se repite
media truncada	media calculada con el 90% central de los datos	`mean(x,trim=10/100)`
rango medio	$rm=\dfrac{min\{x\}-max\{x\}}{2}$	`max(x)-min(x)`
media geométrica	$(x_{1} \times x_{2} \times x_{3} .... x_{n})^{1/n}$
media armónica	$\dfrac{n}{\dfrac{1}{x_{1}}+\dfrac{1}{x_{2}}+\dfrac{1}{x_{3}}+...+\dfrac{1}{x_{n}}}$
dispersión
rango	$r= max\{x\}-min\{x\}$	`max(x)-min(x)`
varianza	$s^{2} = \dfrac{1}{n-1} \displaystyle\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}$	`var(x)`
desviación estandar	$s = \sqrt{s^{2}}$	`sd(x)`
coeficiente de variación	$cv= \dfrac{s}{\bar{x}} \times 100$ %	`sd(x)/mean(x)*100`
forma
coeficiente de curtosis	$\displaystyle\dfrac{Q_{3}-Q_{1}}{P_{90}-P_{10}}$	`rapportools::kurtosis(bpe$promedio)`
coeficiente de asimetría	$\displaystyle\dfrac{3(\bar{x}-Me)}{s}$	`rapportools::skewness(bpe$promedio)`
percentil 25	$X_{n \times 0.25}$	`quantile(x,0.25)`
percentil 50	$X_{n \times 0.50}$	`quantile(x,0.50)`
percentil 75	$X_{n \times 0.75}$	`quantile(x,0.75)`
rango intercuartílico	$Q_{3}-Q_{1}$

Ejemplo

Nivel de ansiedad

Los siguientes datos corresponden al nivel de ansiedad de un grupo de estudiantes de la universidad valorada antes de la presentación del primer examen parcial. El investigador a cargo del proyecto utilizó una prueba para medir el nivel de ansiedad que permite puntajes entre 0 y 100. Los valores inferiores a 50 puntos se consideran como nivel bajo . Entre 50 y 80 , nivel medio y superiores a 80 se consideran altos.

Otra variable importante en el análisis corresponde a la facultad a la que pertence el estudiante

Facultad de Ingeniería y Ciencias
Facultad de Ciencias Económicas y Administrativas
Facultad de Humanidades
Facultad de Salud

Los resultados obtenidos se presenta a continuación :

nivans=c(28,33,34,36,38,38,41,41,45,45,46,46,47,47,48,48,49,50,51,51,51,52,53,53,
         53,54,54,54,55,55,55,56,56,56,57,57,58,60,61,61,61,62,63,64,64,65,65,65,
         65,65,66,67,67,68,68,68,69,69,69,70,70,71,74,77,77,78,79,79,80,82,85,89,
         90,96,58,90,77,71,41,55,53,65,57,56,68,56,50,36,70,57,41,62,48,67,33,52,
         65,67,79,55,34,46,55,56,47,69,61,54,74,47,64,79,85,61,28,46,65,51,49,45,
         78,96,68,38,77,34,69,69,38,65,63,68,48,53,82,61,51,45,66,65,64,70,89,51,
         54,53,80,54,60,53)

fac=c(2,1,2,2,4,3,4,2,4,2,4,1,1,1,1,1,1,2,3,3,3,3,1,2,1,2,2,1,1,2,3,2,3,2,2,3,3,
      1,1,1,2,1,2,2,2,3,1,1,3,1,4,3,1,3,2,1,2,3,4,3,2,3,4,4,1,3,4,4,2,2,1,4,2,1,
      2,4,1,1,1,3,4,1,1,1,1,1,3,3,3,3,1,1,1,2,2,1,3,1,1,1,3,2,2,2,2,1,2,2,1,3,2,
      1,2,2,2,4,2,1,3,4,1,1,3,1,2,2,2,1,3,3,1,1,2,2,3,3,3,1,4,3,1,2,4,2,2,1,2,3,
      2,2)

data=data.frame(fac, nivans) # forma base de datos

Tablas de frecuencia

Construya una tabla de frecuencia que le permita establecer las frecuencias en cada uno de los rangos descritos y analice los resultados obtenidos.

Primera forma : Utilizando el paquete agricolae

h2=with(data,graph.freq(nivans,plot=FALSE))
t2=table.freq(h2);
colnames(t2) = c("  LI  ", "  LS  ", "marca clase'", "Frec.Abs","Frec.Rel", "Frec.Abs.Ac","Frec.Rel.Ac")
t2

    LI     LS   marca clase' Frec.Abs Frec.Rel Frec.Abs.Ac Frec.Rel.Ac
1   28.0   36.5        32.25        9      6.0           9         6.0
2   36.5   45.0        40.75        8      5.3          17        11.3
3   45.0   53.5        49.25       35     23.3          52        34.7
4   53.5   62.0        57.75       32     21.3          84        56.0
5   62.0   70.5        66.25       40     26.7         124        82.7
6   70.5   79.0        74.75       10      6.7         134        89.3
7   79.0   87.5        83.25       10      6.7         144        96.0
8   87.5   96.0        91.75        6      4.0         150       100.0

Segunda forma : utilizando la función hist

h=hist(data$nivans, breaks = c(20,29.99,39.99,49.99,59.99,69.99,79.99,89.99,100), plot=FALSE)
LI=round(h$breaks[1:8],0) 
LS=round(h$breaks[2:9],0) 
ni=h$counts
hi=h$counts/150
Ni=cumsum(h$counts)
Hi=Ni/150

t=data.frame(LI,LS,ni,hi,Ni,Hi)
t

  LI  LS ni         hi  Ni         Hi
1 20  30  2 0.01333333   2 0.01333333
2 30  40 11 0.07333333  13 0.08666667
3 40  50 22 0.14666667  35 0.23333333
4 50  60 41 0.27333333  76 0.50666667
5 60  70 44 0.29333333 120 0.80000000
6 70  80 18 0.12000000 138 0.92000000
7 80  90  8 0.05333333 146 0.97333333
8 90 100  4 0.02666667 150 1.00000000

Tercera forma : utilizando la funciones : cut y cbind

nivans1=cut(data$nivans, breaks = c(20,29.99,39.99,49.99,59.99,69.99,79.99,89.99,100))
t2=table(nivans1)
t2=cbind(t2, t2/sum(t2),cumsum(t2), cumsum(t2)/sum(t2))
colnames(t2)=c("n","h","N","H")
t2

          n          h   N          H
(20,30]   2 0.01333333   2 0.01333333
(30,40]  11 0.07333333  13 0.08666667
(40,50]  22 0.14666667  35 0.23333333
(50,60]  41 0.27333333  76 0.50666667
(60,70]  44 0.29333333 120 0.80000000
(70,80]  18 0.12000000 138 0.92000000
(80,90]   8 0.05333333 146 0.97333333
(90,100]  4 0.02666667 150 1.00000000

Cálculos las estadísticas descriptivas del nivel de ansiedad y describa los resultados en un párrafo

summarytools::descr(data$nivans)

Error in match.call(f, call): ... used in a situation where it does not exist

Descriptive Statistics  

                    data$nivans
----------------- -------------
             Mean         59.51
          Std.Dev         14.13
              Min         28.00
               Q1         51.00
           Median         58.00
               Q3         68.00
              Max         96.00
              MAD         14.08
              IQR         17.00
               CV          0.24
         Skewness          0.19
      SE.Skewness          0.20
         Kurtosis         -0.20
          N.Valid        150.00
                N        150.00
        Pct.Valid        100.00

El grupo observado corresponde a un total de 150 estudiantes de las cuatro facultades de la universidad (aun no estaba la Facultad de Habitat) y presentan un valor promedio de 59.5 puntos que corresponde a un nivel medio. Su coeficiente de variación (24%) muestra un poco de heterogeneidad en los valores alcanzados por los estudiantes, mientras que su forma se aproxima a una distribución simétrica

Tabla de frecuencias para variables cualitativas utilizando del paquete summarytools la función freq

data$fac[data$fac==1]="Facultad de Ingeniería y Ciencias"
data$fac[data$fac==2]="Facultad de Ciencias Económicas y Administrativas"
data$fac[data$fac==3]="Facultad de Humanidades"
data$fac[data$fac==4]="Facultad de Salud"
summarytools::freq(data$fac, cumul = FALSE)

Error in match.call(f, call): ... used in a situation where it does not exist

Frequencies  

                                                          Freq   % Valid   % Total
------------------------------------------------------- ------ --------- ---------
      Facultad de Ciencias Económicas y Administrativas     48     32.00     32.00
                                Facultad de Humanidades     34     22.67     22.67
                      Facultad de Ingeniería y Ciencias     51     34.00     34.00
                                      Facultad de Salud     17     11.33     11.33
                                                   <NA>      0                0.00
                                                  Total    150    100.00    100.00

Los reultados indican una mayor proporción de estudiantes de la Facultad de Ingenieria y Ciencias (34%), mientras que la Facultad de Salud la menor (11.3%)

Video

Lo podemos lograr…

Daniel Enrique González Gómez

Imagen tomada de : https://pixabay.com/es/images/search/paisaje/

Grupo 1	Grupo 1
\(\bar{x} = 20\) años	\(\bar{x} = 20\) años
\(r = 4\) años	\(r = 38\) años

Unidad 1.1

dgonzalez

¿Que es un indicador?

Tablas de frecuencia

Tablas de frecuencia para variables cualitativas

Tablas de frecuencia para variables cuantitativas

Rango percentil

Reto :

Diagrama de cajas

Renumen

Indicadores de los Datos

Indicadores de Centro

Media aritmética

Mediana

Moda

Otras medidas de centro

Media truncada

Rango medio

Media geométrica

Media armónica

Problema reconocimiento de grupo

Indicadores de Dispersión

Rango

Varianza

Propiedades de la varianza

Desviación estándar

Coeficiente de variación

Indicadores de Forma

Curtosis

Asimetría o sesgo

Formulario

Ejemplo

Nivel de ansiedad

Tablas de frecuencia

Video

Lo podemos lograr…

Daniel Enrique González Gómez

Estadística	fórmula	código R
centro
media aritmética	\(\displaystyle\dfrac{1}{n}\sum_{i=1}^{n} x_{i}\)	`mean(x)`
mediana	\(Me = P_{50} = X_{n+1/2}\)	`median(x)`
moda	\(Mo\) dato que más se repite
media truncada	media calculada con el 90% central de los datos	`mean(x,trim=10/100)`
rango medio	\(rm=\dfrac{min\{x\}-max\{x\}}{2}\)	`max(x)-min(x)`
media geométrica	\((x_{1} \times x_{2} \times x_{3} .... x_{n})^{1/n}\)
media armónica	\(\dfrac{n}{\dfrac{1}{x_{1}}+\dfrac{1}{x_{2}}+\dfrac{1}{x_{3}}+...+\dfrac{1}{x_{n}}}\)
dispersión
rango	\(r= max\{x\}-min\{x\}\)	`max(x)-min(x)`
varianza	\(s^{2} = \dfrac{1}{n-1} \displaystyle\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}\)	`var(x)`
desviación estandar	\(s = \sqrt{s^{2}}\)	`sd(x)`
coeficiente de variación	\(cv= \dfrac{s}{\bar{x}} \times 100\) %	`sd(x)/mean(x)*100`
forma
coeficiente de curtosis	\(\displaystyle\dfrac{Q_{3}-Q_{1}}{P_{90}-P_{10}}\)	`rapportools::kurtosis(bpe$promedio)`
coeficiente de asimetría	\(\displaystyle\dfrac{3(\bar{x}-Me)}{s}\)	`rapportools::skewness(bpe$promedio)`
percentil 25	\(X_{n \times 0.25}\)	`quantile(x,0.25)`
percentil 50	\(X_{n \times 0.50}\)	`quantile(x,0.50)`
percentil 75	\(X_{n \times 0.75}\)	`quantile(x,0.75)`
rango intercuartílico	\(Q_{3}-Q_{1}\)