Problemas

Problema 1

Para el siguiente grupo de variables defina para cada caso el tipo de variable y la escala de medición

1.	Número de botellas plásticas producidas diariamente en un proceso de moldeado, en Agua Limpia S.A
2.	Número de defectos observados por gabinete para equipo de cómputo de una distribuidora
3.	Tiempo de respuesta a los pedidos telefónicos en un restaurante
4.	Desperdicio de hojas por día en la fotocopiadora Copiamenos
5.	Tipo de defectos en tarjetas de circuito impreso de un lote de producción.
6.	Temperatura de cocción de la meladura en un proceso de producción de azúcar.
7.	Espesor de las piezas de metal producido en la empresa Tornos S.A.
8.	Técnica de mezclado de cemento tipo A por lote en la Cementera del Norte
9.	Cantidad de corriente en microamperios por cada medición en un cinescopio
10.	Grado de satisfacción de los clientes ante el servicio de mantenimiento de un taller mecánico
11.	Nota obtenida en el examen de estadística
12.	Nivel de estrés de un estudiante antes de una presentar una prueba escrita
13.	Número de llamadas de servicio al cliente atendidas por día en una empresa de telecomunicaciones.
14.	Porcentaje de cumplimiento de las metas de producción mensual en una fábrica de automóviles.
15.	Duración en minutos de las reuniones de equipo en una empresa tecnológica.
16.	Número de quejas recibidas por semana en una cadena de supermercados.
17.	Calidad del aire medida en partículas por millón (ppm) en una zona industrial.
18.	Nivel de satisfacción de los empleados con el ambiente laboral en una encuesta anual.
19.	Cantidad de productos defectuosos detectados por turno en una línea de ensamblaje.
20.	Tiempo en segundos para cargar una página web en diferentes navegadores.
21.	Volumen de ventas mensuales en una tienda en línea.
22.	Temperatura promedio diaria registrada en una ciudad durante el verano.
23.	Número de accidentes laborales reportados por mes en una planta manufacturera.
24.	Grado de conocimiento sobre seguridad informática de los empleados después de un taller de capacitación.

Problema 2

Indique el concepto referido en cada uno de los siguientes enunciados:

1.	Divide la muestra en dos partes de igual proporción.
2.	Mide la simetría de la distribución de datos alrededor de la media.
3.	Describe la dispersión de los datos en torno a la media en términos relativos.
4.	Mide la concentración de los datos alrededor de la mediana.
5.	Se obtiene al calcular el cociente entre la desviación estándar y la media aritmética.
6.	Proporciona una medida de la dispersión de los datos respecto a la media.
7.	Mide la diferencia entre el valor del tercer cuartil y el primer cuartil.
8.	Mide la dispersión de los datos respecto a la media sin considerar el signo de las desviaciones.
9.	Calcula la diferencia entre el valor máximo y el valor mínimo en un conjunto de datos.
10.	Representa el valor más frecuente en un conjunto de datos.
11.	Estima la tendencia central en una muestra y es muy sensible a los valores extremos.
12.	Describe el grado de inclinación de la distribución de datos en torno a la media.
13.	Se obtiene al ordenar los datos y seleccionar el valor que se encuentra en la posición central.
14.	Se obtiene al restar el primer cuartil del tercer cuartil en una distribución de datos.
15.	Mide el grado de dispersión de los datos en relación con su media aritmética.
16.	Indica el promedio de los valores absolutos de las diferencias entre cada valor y la media.
17.	Proporciona una medida de la dispersión de los datos que es independiente de la unidad de medida.
18.	Mide la variabilidad de los datos en una muestra mediante la raíz cuadrada de la varianza.
19.	Representa la suma de los valores observados dividida por el número total de observaciones.
20.	Mide la dispersión relativa de los datos utilizando el coeficiente de variación.
21.	Describe la dispersión de los datos utilizando el rango intercuartil.
22.	Indica el valor que divide una muestra en dos mitades iguales.
23.	Se obtiene al calcular la diferencia entre el tercer cuartil y la mediana.
24.	Mide el grado de asimetría de una distribución en relación con su media y desviación estándar.
25.	Proporciona una medida de la forma de la distribución, indicando si es más alta y delgada o más baja y ancha.
26.	Indica el valor que se encuentra en la posición de la mediana en un conjunto de datos ordenados.
27.	Describe la distribución de los datos en torno a la media utilizando la curtosis.
28.	Mide la dispersión de los datos en relación con su media utilizando el coeficiente de Pearson.
29.	Indica la diferencia entre el valor máximo y el primer cuartil en una distribución de datos.

Problema 3

Responda F (Falso) o V (Verdadero), justificando la respuesta en caso de ser Falsa.

1.	La desviación estándar del conjunto de valores 2, 2, 2, 2 y 2 es 2.
2.	En una distribución de frecuencias acampanada, el rango de los datos es aproximadamente igual a seis desviaciones estándar.
3.	Dos conjuntos de datos de tamaños \(n_1\) y \(n_2\) tienen respectivamente promedios \(\bar{x}_{1}\) y \(\bar{x}_{2}\), a partir de esta información, se puede obtener el respectivo estadístico del total de datos (\(\bar{x}\))
4.	Al hacer una gráfica, las frecuencias deben representarse en el eje de la ordenada.
5.	El histograma, es una presentación muy efectiva de las distribuciones de frecuencias.
6.	El polígono de frecuencias, es especialmente apto para comparar diferentes distribuciones.
7.	Una variable discreta puede ser representada mediante un histograma
8.	El diagrama de barras se utiliza para representar datos continuos.
9.	La relación de escalas en una gráfica debe de ser 1:1
10.	Las gráficas se representan en el primer cuadrante del plano cartesiano.
11.	Si multiplicamos la variable por una constante, el coeficiente de variación se altera.
12.	La varianza de una constante por una variable es igual a la varianza de la variable.
13.	Al sumar 4 a cada uno de los números de la serie : 2, 6, 5, 9, 1 se obtiene la serie 6, 10, 9, 13 y 5. Las series tienen igual varianza, distinta media y diferente coeficiente de variación.
14.	La media aritmética es siempre mayor que la mediana en una distribución sesgada a la derecha.
15.	En una distribución normal, aproximadamente el 95% de los datos se encuentra dentro de dos desviaciones estándar de la media.
16.	La mediana es afectada por los valores extremos en un conjunto de datos.
17.	La moda es el único promedio que puede tener más de un valor en un conjunto de datos.
18.	El coeficiente de correlación de Pearson puede variar entre -1 y 1.
19.	Si todos los valores de un conjunto de datos se multiplican por una constante, la media se multiplica por la misma constante.
20.	La desviación estándar de una constante es siempre cero.
21.	La suma de los cuadrados de las desviaciones respecto a la media es siempre mayor o igual a cero.
22.	En un diagrama de caja y bigotes, el bigote inferior representa el primer cuartil.
23.	La probabilidad de que ocurra un evento imposible es uno.
24.	La covarianza mide la relación lineal entre dos variables.
25.	El coeficiente de determinación (R²) indica la proporción de la variabilidad total de una variable que es explicada por la variabilidad de otra variable.
26.	Una distribución bimodal tiene dos picos o modas.
27.	Si la media es igual a la mediana y a la moda, la distribución es simétrica.
28.	La media geométrica es siempre mayor que la media aritmética.
29.	El intervalo intercuartílico es la diferencia entre el primer cuartil y el tercer cuartil.
30.	Una variable continua puede asumir un número infinito de valores dentro de cualquier intervalo.

Estas nuevas preguntas siguen el mismo formato y estilo de las proporcionadas inicialmente.

Problema 4

Elabore un gráfico para representar adecuadamente la siguiente información:

Durante 5 meses se construyen 134 kilómetros de carretera en la siguiente forma: En el primer mes, 3.60% del total del proyecto; en el segundo més un 7.60% del total; en el tercer més, el 15.3% del total; en el cuarto mes 24.5% del total y en último mes, el 49% restante.
El grupo de Probabilidad y Estadística a cargo de un profesor está conformado por : 9 estudiantes de Ingeniería Electrónica, 6 de Ingeniería de Sistemas, 25 de Ingeniería Civil, 19 de Negocios Internacionales 8 de Biología y 3 de Ingeniería Mecánica. De los que estudian Ingeniería Electrónica 6 son hombres, de los matriculados en Ingeniería de Sistemas 2 son mujeres, de los que estudian Ingeniería Civil 18 son hombres, de los que estudian Negocios internacionales 16 son mujeres, de los que estudian Biología 5 son mujeres y finalmente de los que estudian Ingeniería Mecánica 2 son hombre.
Una consulta en tiendas en linea para memorias USB 128GB arrojó lo siguientes valores:

x=c(60,63,64,67,68,68,68,70,70,71,71,72,72,72,73,73,74,74,75,75,75,75,75,76,76,77,77,79,80,83,83,84,85,86,87,88,88,89,89,91)
stem(x)


  The decimal point is 1 digit(s) to the right of the |

  6 | 034
  6 | 7888
  7 | 00112223344
  7 | 5555566779
  8 | 0334
  8 | 5678899
  9 | 1

La clasificación de los empleados de una empresa por cargo es la siguiente: un Administradores, tres Ingenieros, treinta operarios, ocho celadores, dos contadores, tres secretarias, cinco supervisores, treinta y seis vendedores.

Problema 5

Un vendedor convierte los pesos de los paquetes que se producen en su empresa de libras a kilogramos (\(1\) kg \(\simeq\) 2.2 lb.). Como afecta esta conversión la media y la desviación estándar?.

NOTA

\(\bar{x}=\frac{1}{n}\sum x_{i}\),
\(s=\sqrt{s^2}\),
\(s^2=\frac{1}{(n-1)}\sum (x_{i}-\bar{x})^{2}\)

Problema 6

Para analizar la rapidez con que una máquina etiqueta las botellas en una compañía de jugos, se decide hacer seguimiento al número de botellas etiquetadas por día. A partir de los resultados procesados en R presente un análisis estadístico para el número de botellas etiquetadas por día

summarytools::descr(x)

Error in match.call(f, call): ... used in a situation where it does not exist

Descriptive Statistics  

                         x
----------------- --------
             Mean    76.08
          Std.Dev     7.82
              Min    60.00
               Q1    71.00
           Median    75.00
               Q3    83.00
              Max    91.00
              MAD     7.41
              IQR    12.00
               CV     0.10
         Skewness     0.20
      SE.Skewness     0.37
         Kurtosis    -0.81
          N.Valid    40.00
                N    40.00
        Pct.Valid   100.00

Punto 11 pag. 34 notas Alonso

Problema 7

El director de la asociación de comerciantes de tomates del Valle del Cauca estudia el comportamiento de las ventas diarias de los últimos meses para una muestra de 60 nuevos microempresarios en la región. Dos de las variables más importantes a tener en cuenta para el estudio fueron: Ventas (meses Mayo y Junio) y el nivel tecnológico de la empresa. La siguiente información corresponde a las ventas:

May = c(14.3, 14.4, 11.1, 11.2, 11.4, 11.4, 11.4, 11.4, 10.0, 10.5, 10.5, 10.6, 10.7, 12.1, 12.3, 12.4, 12.8,  9.3,  9.2,  9.2, 9.1,  8.4,  8.5,  7.2,  7.1,  6.2, 13.7, 13.8, 15.0, 10.0)

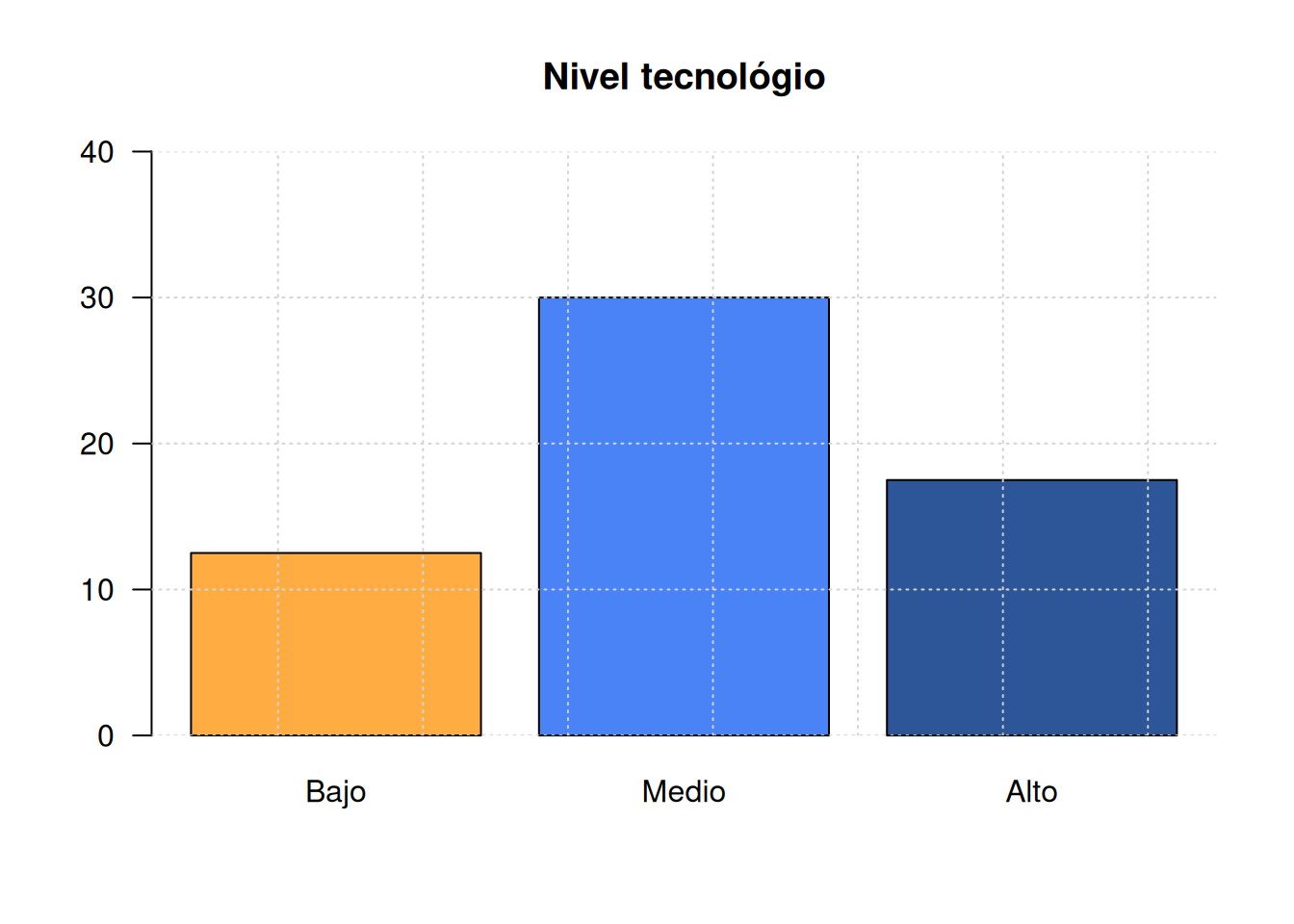
Jun = c(12.0, 12.0, 12.0, 12.7, 12.8, 12.9, 8.0, 8.0, 13.2, 13.3, 13.5, 13.6, 11.0, 11.5, 11.6, 11.9, 10.4, 10.3, 10.7,  9.0, 9.2,  7.4,  7.7,  6.1,  5.9, 14.3, 14.2, 14.8, 15.1, 15.2)

El nivel tecnológico de los 60 distribuidores mostró el siguiente comportamiento tomados en el estudio

Error in match.call(f, call): ... used in a situation where it does not exist

Descriptive Statistics  

                       Jun      May
----------------- -------- --------
             Mean    11.34    10.84
          Std.Dev     2.65     2.22
              Min     5.90     6.20
               Q1     9.20     9.20
           Median    11.95    10.90
               Q3    13.30    12.30
              Max    15.20    15.00
              MAD     2.37     2.30
              IQR     3.80     3.03
               CV     0.23     0.20
         Skewness    -0.48    -0.07
      SE.Skewness     0.43     0.43
         Kurtosis    -0.87    -0.66
          N.Valid    30.00    30.00
                N    30.00    30.00
        Pct.Valid   100.00   100.00

De acuerdo con la información anterior, responda falso o verdadero a las siguientes premisas. En caso de ser falsa justifique su respuesta.

a.	La variable ventas mensuales se mide en escala de razón
b.	Las ventas de 6.2 millones representan un dato atípico, para la información de Mayo
c.	Las ventas de Mayo son más homogéneas que las de Junio
d.	La mediana de las ventas en el mes de Junio es de 11.15
e.	La varianza para el mes de Junio es de 5.21
f.	Aproximadamente el 68% de las ventas de Junio están en el intervalo [8.7 ; 13.3]. Nota: el intervalo incluye los valores 8.7 y 13.3.
g.	Si el estado cobra un impuesto sobre las ventas del 16%, el promedio del impuesto en Junio es de 1.75
h.	En la variable nivel tecnológico, el promedio es: \(\dfrac{12.5+30+17.5}{3}\)
i.	El cuartil 1 \(Q_{1}\) para las ventas de Mayo es 8.0
j.	El tipo de estudio corresponde a la Estadística Inferencial ya que se realizó muesteo
k.	La variable nivel tecnológico de la empresa se clasifica como nominal
l.	30 empresas tienen un nivel tecnológico medio
m.	Las ventas de Junio muestran sesgo negativo

Tomado de Arroyo(2012)

Problema 8

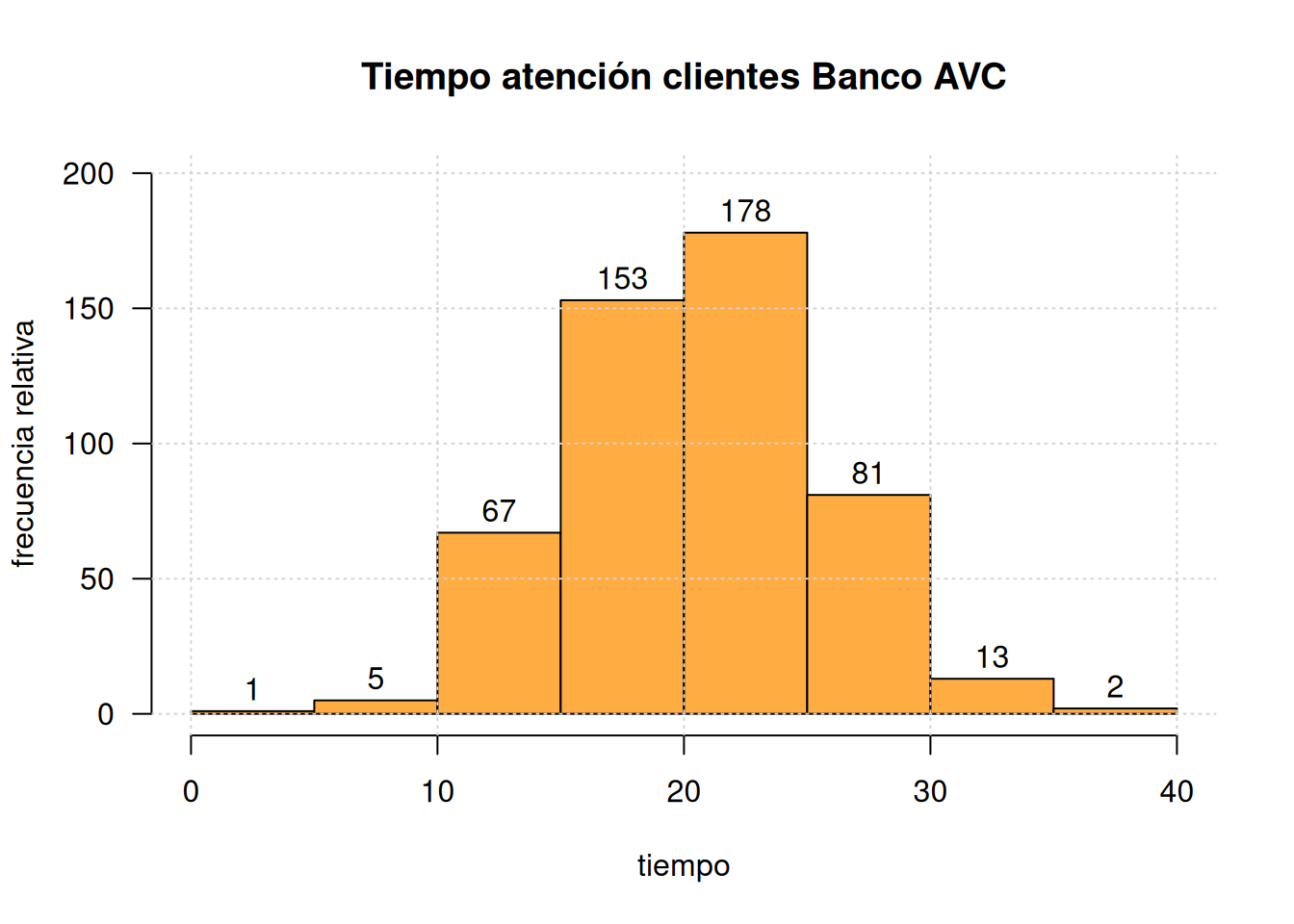
A partir del siguiente gráfico de los tiempos de atención en una entidad bancaria determine la media y la mediana (n=500 clientes). Se puede afirmar que la distribución del tiempo de atención es asimétrica positiva?. Se desea establecer los porcentajes de clientes atendidos en los rangos bajos (menos de 10 min), medios (entre 10 min y 12 min), altos (más de 12 min), con el fin de evaluar si en su mayoría los tiempos se concentran en el rango medio. Verifique si esta afirmación es correcta.

Problema 9

En un estudio realizado para investigar la distribución del tiempo de frendo total ( tiempo de reacción más tiempo para pasar del acelerador al freno, en ms) en condiciones reales de manejo a 60 km/h se obtuvo el siguiente resumen de la distribución de los tiempos:

Descriptive Statistics  
N: 450  
x : frenado
-------------------------
Mean       529.35
Std.Dev     94.39
Min        277.14
Q1         464.50
Median     527.85
Q3         591.93
Max        804.80
MAD         94.30
IQR        127.33
CV           0.18
Skewness     0.06
SE.Skewness  0.12
Kurtosis    -0.23
N.Valid    450.00
Pct.Valid  100.00

¿Qué se concluye en relación con la forma de estos datos?. Acompañe su análisis de un diagrama de cajas

Problema 10

Los pesos en libra de 54 paquetes de hamburguesas fueron obtenidos en el mostrador de un supermercado de cadena de la ciudad (mín = 0.75, máx = 1.41 )


  The decimal point is 1 digit(s) to the left of the |

   7 | 55
   8 | 3367799999
   9 | 22366667778899
  10 | 668888
  11 | 22224444778888
  12 | 4488
  13 | 88
  14 | 11

[1] 56.83

\(\displaystyle\sum_{i=1}^{54}(x_{i}-\bar{x})=0\)

\(\displaystyle\sum_{i=1}^{54}x_{i} =56.83\)

\(\displaystyle\sum_{i=1}^{54}(x_{i}-\bar{x})^{2}=1.429387\)

\(\displaystyle\sum_{i=1}^{54}x_{i}^2 = 61.2377\)

Construya un diagrama de cajas y a partir de este resultado determine si su forma es simétrica

Para construir el diagrama de cajas se emplean los cuartiles (\(Q_{1}\), \(Q_{2}\) y \(Q_3\)). Ellos determinan la caja central del diagrama. Las lineas a lado y lado

a.	Se puede afirmar que existen datos atípicos?
b.	Podría afirmarse que más del 20% de los paquetes tienen un peso superior a 1.11 libras?
c.	Realice un breve descripción de la información obtenida

(Tomado de Mendenhall 2006)

Problema 11

El valor alcanzado por estudiantes en un test para medir el razonamiento deductivo mediante una prueba de personalidad de Millón (MPIS) se presenta en la siguiente tabla:

Edad	Marca de clase	Frecuencia Absoluta	Frecuencia Relativa	Frec. Acum. Absoluta	Frec. Acum. Relativa
[0-10)		3
[10-20)		6
[20-30)		7
[30-40)		12
[40-50)		3

A partir de la información responda los siguientes interrogantes:

a.	Los valores obtenidos se pueden considerar como valores homogéneos?
b.	La distribución representada por la tabla se puede considerar como simétrica?
c.	Qué indicador de centro podría ser más apropiado para representar los datos? Justifique su respuesta.
d.	Describa los resultados obtenidos en la medición.

Problema 12

Los tiempo en minutos de demora en la entrega de pedidos por parte de dos proveedores de insumos para laboratorio que llamaremos \(P_{A}\) y \(P_{B}\) son los siguientes :

PA=c(13,44,10,11,20,29,30,44,56,63,70,82); cat("Proveedor A: ", PA, "\n")

Proveedor A:  13 44 10 11 20 29 30 44 56 63 70 82

PB=c(25,14,20,22,30,33,40,45,49,52,55,58); cat("Proveedor B: ", PB, "\n")

Proveedor B:  25 14 20 22 30 33 40 45 49 52 55 58

Con base en la información, cuál proveedor escogería? Justifique su respuesta

(Tomado de Arroyo(2012))

Problema 13

Un una fabrica de de jabones para el aseo personal realizó un estudio con el objetivo de mejorar una linea de este producto, mediante la medición de los pesos (en onzas) de 50 barras.

Los resultados obtenidos y algunos cálculos sobre los datos se presentan a continuación :

x = c(20.3, 19.2, 18.8, 18.5, 18.5, 18.3, 18.3, 18.2, 18.1, 17.7, 17.6,
14.4, 17.4, 17.4, 17.3, 17.3, 17.1, 17.0, 16.6, 16.5, 16.5,  16.5,
16.4, 16.3, 16.2, 16.2, 16.1, 15.9, 15.9, 15.8, 15.8, 15.7, 15.6,
15.6, 15.2, 15.1, 14.8, 14.6, 14.3, 14.3, 14.1, 13.8, 13.7, 13.6,  
13.3, 13.1, 12.8, 12.7, 12.6,  11.6)
stem(x)


  The decimal point is at the |

  11 | 6
  12 | 678
  13 | 13678
  14 | 133468
  15 | 126678899
  16 | 122345556
  17 | 01334467
  18 | 1233558
  19 | 2
  20 | 3

Suma x  :     798.6 
Suma x2 :   12941.46 
Suma x3 :  212596.4 
Suma x4 : 3537246 
sd      :       1.949468

Por política de la empresa, el peso del producto debe estar en un 90% de los casos entre mas o menos dos onzas al rededor del peso especificado en la etiquete del producto (16.0 onzas). Un segundo criterio importante es el de establecer si en los datos obtenidos se presentan datos atípicos y si los valores se pueden clasificar como homogéneos, teniendo como referencia un indicador del 10%. En caso de no cumplimiento de los criterios de calidad será necesario detener la producción y llamar a la empresa de mantenimiento para que realice los ajustes necesarios.

Debido a que la muestra obtenida constituye una muestra representativa del proceso, el director de la empresa le pide le ayude a validar los resultados y le indique que decisión debe tomarse a partir de la información obtenida

Problema 14

Un grupo de estudiantes de la universidad, preocupados por el incremento del uso de los vapeadores entre los jóvenes, realizan un estudio acerca de los efectos de su uso sobre los patrones de sueño. Para estudiar el problema miden el tiempo en minutos que se tarda un joven en quedarse dormido. Con el fin de tener un grupo de referencia, la observación se realiza en jóvenes que utilizan el vapeador y los que lo usan. Los resultados obtenidos fueron los siguientes

# Vapeadores  
x = c(69.3, 56.0, 22.1, 47.6, 53.2, 48.1, 52.7, 34.4, 60.2, 43.8, 23.2, 33.8, 45.5, 55.2, 48.2)
cat("x = ", x, "\n")

x =  69.3 56 22.1 47.6 53.2 48.1 52.7 34.4 60.2 43.8 23.2 33.8 45.5 55.2 48.2

# No vapeadores  
y = c(28.6, 25.1, 26.4, 34.9, 29.3, 28.4, 38.5, 30.2, 30.6, 31.8, 41.6, 21.1, 36.0, 37.9, 13.9)
cat("y = ",y, "\n")

y =  28.6 25.1 26.4 34.9 29.3 28.4 38.5 30.2 30.6 31.8 41.6 21.1 36 37.9 13.9

cat("\n")

summarytools::descr(x)

Error in match.call(f, call): ... used in a situation where it does not exist

Descriptive Statistics  

                         x
----------------- --------
             Mean    46.22
          Std.Dev    13.14
              Min    22.10
               Q1    34.40
           Median    48.10
               Q3    55.20
              Max    69.30
              MAD    10.53
              IQR    15.10
               CV     0.28
         Skewness    -0.37
      SE.Skewness     0.58
         Kurtosis    -0.75
          N.Valid    15.00
                N    15.00
        Pct.Valid   100.00

summarytools::descr(y)

Error in match.call(f, call): ... used in a situation where it does not exist

Descriptive Statistics  

                         y
----------------- --------
             Mean    30.29
          Std.Dev     7.13
              Min    13.90
               Q1    26.40
           Median    30.20
               Q3    36.00
              Max    41.60
              MAD     6.97
              IQR     8.05
               CV     0.24
         Skewness    -0.49
      SE.Skewness     0.58
         Kurtosis    -0.27
          N.Valid    15.00
                N    15.00
        Pct.Valid   100.00

De a cuerdo con los valoresa obtenidos es posible afirmar que existen diferencias en los dos grupos observados con referencia al tiempo que se requiere para quedarse dormido?

Problema 15

Determine el valor de verdad (verdadera - V, falsa - F) para cada una de las siguientes afirmaciones. En cada caso justifique su respuesta:

( ) Al construir una gráfica barras, las frecuencia deben representarse en el eje de las ordenadas.
( ) El histograma, es una representación muy efectiva de las frecuencias obtenidas en una variable categórica.
( ) El polígono de frecuencias, es especialmente apto para comparar datos con diferentes formas.
( ) Una variable cualitativa en escala ordinal puede ser representada mediante un histograma.
( ) El diagrama de barras se emplea para representar datos continuos.
( ) La relación de las escalas en un diagrama de puntos debe ser 1:1 .
( ) Las gráficas de puntos o de dispersión se deben representar en el primer cuadrante del plano cartesiano.
( ) Si sumamos una constante a la mitad de los datos, la media se altera en la mitad de la constante.
( ) El gráfico circular se emplea para representar variables cualitativas medidas en escala ordinal.

Problema 16

Diez estudiantes que realizan practica estudiantil reciben un salario mensual durante su trabajo en millones de pesos :

x= c(1.1, 1.2, 1.4, 1.7, 1.9, 1.3, 1.6, 1.4, 1.3, 1.6)
x

 [1] 1.1 1.2 1.4 1.7 1.9 1.3 1.6 1.4 1.3 1.6

Calcules la media y la mediana.
¿Cual de los indicadores es más representativo de la información como indicador de tendencia central? Justifique su respuesta.

Problema 17

El peso de 80 artículos es de 130 kgs. Si 60 de ellos pesan en promedio 120 kgs. ¿Cual será el peso promedio de los 70 artículos restantes?

Problema 18

Construye un ejemplo específico para el caso de:

Media armónica
Media geométrica
Media ponderada
Media truncada

Problema 19

Una persona que viaja en un vehículo de una ciudad A a una ciudad B, en el viaje de ida la velocidad media es de 40 km/h y de regreso (B -> A) registra una velocidad promedio de 60 km/h. Se pueden calcular los valores de la media y mediana para el viaje completo ?

Problema 20

Describa la relación existente entre la media y la mediana para los siguientes casos :

Forma de los datos acamapnada
Forma de los datos rectangular
Forma de los datos asimétrica positiva
Forma de los datos asimétrica negativa

Realice un bosquejo de su representación gráfica y de la posición de los indicadores de centro.

Problema 21

Supermercados de ventas de alimentos:

El siguiente conjunto de datos incluye información de la última semana de 100 establecimientos sobre sus ventas, costos, utilidad, número de empleados y su estrato socio-económico del barrio donde se encuentran localizados. Realiza un análisis descriptivo de la información suministada, utilizando indicadores de centro, dispersión y forma y graficos que complementen el análisis, que permitan identificar tendencias en las ventas, costos y beneficios , si existe relación entre sus indicadores y su localización, de tal forma que permitan establecer un estado inicial de las empresas para este año.

Información

ventas <-c(41.3, 55.1, 83.4, 61.6, 46.1, 67.4, 59.5, 77.4, 71.7, 61.6, 70.2,  64.1, 61.6, 56.6, 76.8, 65.4, 74.4, 66.4, 62.4, 66.1, 59.6, 45.6,  61.5, 59.7, 49.3, 95.2, 56.0, 75.0, 64.7, 59.3, 51.6, 44.1, 58.2, 52.5, 53.5, 56.0, 59.2, 53.7, 51.3, 59.6, 51.0, 48.7, 49.4, 94.9, 77.0, 56.2, 63.0, 62.6, 56.9, 48.5, 68.0, 50.3, 59.0, 67.6, 46.0, 57.9, 64.9, 61.0, 64.0, 66.2, 51.6, 67.0, 57.6, 68.2, 61.3, 53.7,  71.7, 59.6, 73.9, 66.1, 67.0, 55.8, 64.2, 60.3, 51.2, 68.2, 67.0,60.7, 50.5, 54.5, 54.3, 51.6, 77.1, 53.9, 62.0, 70.5, 61.1, 39.2,  61.3, 56.0, 68.9, 59.7, 53.7, 62.0, 58.4, 69.2, 67.4, 63.8, 55.1, 64.1)

costos =c(35.8, 31.2, 28.7, 39.7, 39.0, 34.8, 25.5, 30.9, 30.0, 37.0, 33.3, 40.9, 38.9, 34.0, 41.5, 30.5, 39.1, 36.0, 29.1, 34.2, 34.3, 45.7, 46.2, 34.1, 39.7, 42.6, 36.8, 39.3, 27.2, 40.7, 41.5, 28.4, 38.3, 31.9, 31.0, 33.9, 39.9, 35.4, 39.8, 44.3, 32.7, 33.3, 34.3, 33.3, 36.9, 42.5, 40.2, 28.3, 30.4, 44.6, 40.7, 26.6, 27.2, 34.7, 39.5, 36.8, 34.5, 42.4, 35.4, 25.6, 43.5, 28.1, 33.0, 29.7, 44.0, 49.3, 39.9, 30.7, 37.2, 36.8, 40.5, 37.4, 25.9, 43.0, 30.2, 34.6, 36.1, 39.9, 28.5, 37.7, 32.7, 40.4, 29.6, 34.0, 34.5, 34.4, 35.8, 28.2, 32.9, 38.6, 47.9, 29.2, 28.0, 31.7, 46.0, 37.8, 38.3, 30.7, 40.7, 39.6)

utilidad = c(22.6, 17.5, 19.5, 19.3, 23.0, 26.4, 23.4, 31.3, 30.9, 22.2, 26.1, 34.4, 29.0, 13.7, 21.4, 29.8, 22.3, 22.0, 20.4, 34.0, 19.9, 20.3, 27.0, 14.9, 36.9, 35.2, 29.0, 13.2, 30.6, 23.8, 31.2, 24.0, 33.3, 26.9,  5.9, 27.8, 31.9, 12.3, 14.8, 36.3, 24.4, 24.7, 28.6, 31.7, 26.9, 17.9, 20.8, 18.2, 33.9, 30.3, 29.3, 10.1, 34.6, 25.6, 27.7, 18.0, 31.6, 12.5, 29.2, 23.0, 24.4, 30.5, 15.3, 23.8, 34.7, 23.5, 24.4, 34.3, 23.6, 11.4, 10.0, 21.5, 31.3, 36.1, 29.7, 23.5, 26.8, 22.8, 29.9, 30.6, 20.3, 23.5, 30.6, 19.5, 32.5, 34.4, 18.9, 30.7, 27.9, 20.5, 25.7, 17.2, 36.0, 19.0, 18.4, 23.4, 30.8, 18.2, 16.8, 33.1)

empleados = c(14, 18, 17, 14, 16, 22, 17, 11,  9,  2, 15, 24, 18, 26, 21, 16,  9, 24, 10, 16, 17, 10, 11, 16, 22, 16, 15, 11, 13, 25,  6, 20, 17,  7, 14, 22, 21, 15, 16,  6, 10, 16, 13, 25, 14, 23, 15, 16,  9, 26, 21, 15, 24, 14,  9,  3, 18, 15, 15, 12, 16, 18, 24, 16, 23, 17, 15, 20, 16, 13, 11, 13, 13,  9, 26, 11,  8, 17, 15, 16, 13, 23, 16, 20, 17, 15, 25, 14, 20, 20, 10, 14, 13, 20, 20, 17, 15, 15, 16, 13)
 
estrato =c(5, 3, 3, 3, 5, 4, 2, 4, 5, 2, 2, 3, 3, 4, 6, 6, 6, 3, 5, 5, 2, 5, 4, 5, 2, 2, 2, 5, 4, 4, 3, 4, 4, 4, 3, 6, 2, 4, 6, 5, 4, 5, 3, 3, 2, 3, 2, 2, 5, 2, 2, 6, 3, 6, 6, 4, 5, 6, 5, 3, 3, 2, 3, 3, 2, 4, 5, 5, 2, 5, 2, 2, 2, 6, 2, 5, 3, 6, 2, 4, 3, 2, 6, 2, 5, 5, 4, 3, 3, 4, 3, 6, 4, 5, 6, 5, 5, 6, 4, 4)

datosENE =data.frame(id=1:100,ventas,costos,utilidad,empleados, estrato)
head(datosENE)

  id ventas costos utilidad empleados estrato
1  1   41.3   35.8     22.6        14       5
2  2   55.1   31.2     17.5        18       3
3  3   83.4   28.7     19.5        17       3
4  4   61.6   39.7     19.3        14       3
5  5   46.1   39.0     23.0        16       5
6  6   67.4   34.8     26.4        22       4

Problema 22

Una característica de calidad importante en un proceso de llenado automático es el peso del producto. Las empresas cuidan que el producto final no tenga pesos por debajo del anunciado en su etiqueta, pues de hacerlo puede incurrir en multas y pérdida de algunos de sus clientes. Por el contrario, si el producto se empaca muy por encima del peso especificado, se estará incurriendo en sobrecostos para la empresa.

Una empresa que comercializa café instantáneo descafeinado, en presentación de 6.5 gramos, tiene dentro sus directrices, al comenzar el día, tomar una muestra de 50 bolsas y medir su peso. Se espera que los resultados estén entre más o menos 1.5 gramos alrededor del valor especificado en la etiqueta. Si el porcentaje de bolsas en la muestra es superior al 95 %, se da inicio al proceso. Si alcanza porcentajes entre el 85 % y 95 %, se debe llamar al ingeniero de planta para que realice los ajustes necesarios. Y finalmente, si se encuentran porcentajes inferiores al 85 % se debe reportar a la empresa de mantenimiento, para que realicen ajustes mayores.

El día de hoy se recogió información de una muestra de 50 bolsas. A continuación se presentan los datos y su representación gráfica.

Realice un breve análisis de la información suministrada y a partir de ellos realice recomendaciones.

   # Diagrama de tallos y hojas, peso del paquete de café instantáneo en gramos
   stem(c(4.3, 4.7, 4.8, 4.8, 4.9, 5.0, 5.1, 5.2, 5.4, 5.5, 5.7, 5.7, 5.8, 5.8, 5.9, 5.9, 6.0, 6.0, 6.1, 6.1, 6.1, 6.1, 6.2, 6.2, 6.2, 6.3, 6.3, 6.4, 6.4, 6.5, 6.5, 6.6, 6.7, 7.0, 7.2, 7.3, 7.4, 7.6, 7.7, 7.8, 8.2, 8.5, 8.7, 8.9))


  The decimal point is at the |

  4 | 3
  4 | 7889
  5 | 0124
  5 | 5778899
  6 | 0011112223344
  6 | 5567
  7 | 0234
  7 | 678
  8 | 2
  8 | 579

# Datos de los pesos de los paquetes de café instantáneo
pesos <- c(4.3, 4.7, 4.8, 4.8, 4.9, 5.0, 5.1, 5.2, 5.4, 5.5, 5.7, 5.7, 5.8, 5.8, 5.9, 5.9, 6.0, 6.0, 6.1, 6.1, 6.1, 6.1, 6.2, 6.2, 6.2, 6.3, 6.3, 6.4, 6.4, 6.5, 6.5, 6.6, 6.7, 7.0, 7.2, 7.3, 7.4, 7.6, 7.7, 7.8, 8.2, 8.5, 8.7, 8.9)

# Construcción de la tabla de frecuencias acumuladas
tabla_frecuencias <- table(cut(pesos, breaks = seq(4.0, 9.0, by = 0.5), right = TRUE))
frecuencia_acumulada <- cumsum(tabla_frecuencias)

# Creación de la ojiva
plot(seq(4.25, 8.75, by = 0.5), frecuencia_acumulada, type = "o", 
     xlab = "Peso del paquete de café (gramos)", ylab = "Frecuencia acumulada", 
     main = "Ojiva del Peso de Paquetes de Café Instantáneo",
     xlim = c(4, 9), ylim = c(0, max(frecuencia_acumulada) + 5),
     col = "blue", pch = 16, las=1)
grid()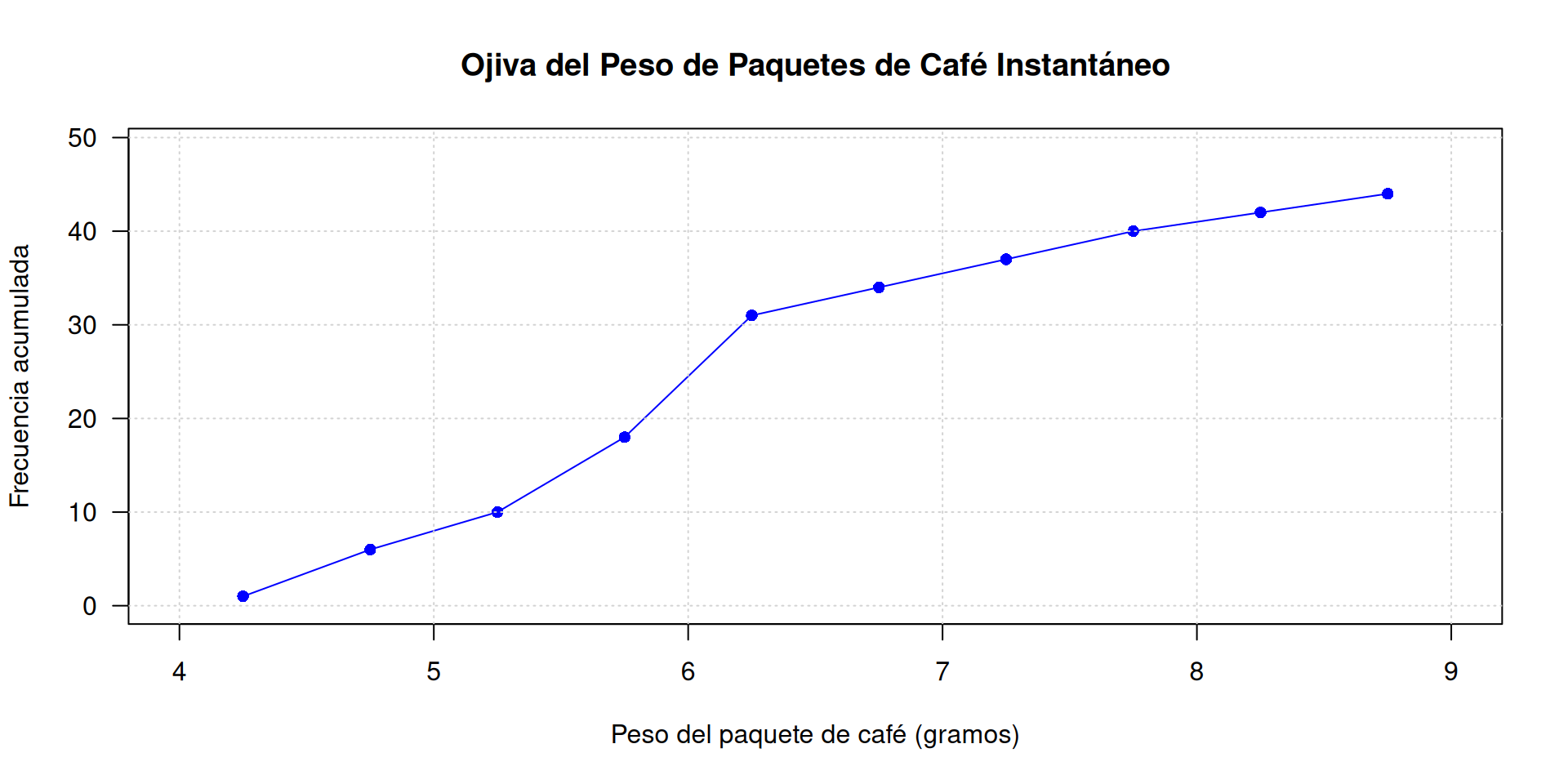

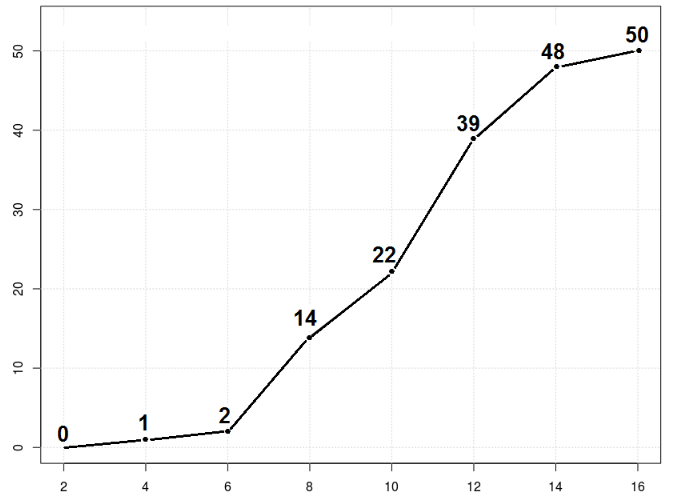
Problema 23

Una de las principales medidas de la calidad de servicio que ofrece una organización y sus departamentos es la rapidez con la que responde a las quejas de sus clientes. El Centro de Servicios Informáticos de la Universidad está interesado en disminuir el tiempo de atención a quejas que se presentan relacionados con el mal funcionamiento de las máquinas virtuales tanto para profesores, colaboradores como para estudiantes que realizan prácticas de investigación. Con el fin de estudiar el comportamiento de este indicador, selecciona una muestra de los tiempos de atención en minutos que se presentan a continuación:

2  | 3
4  | 4
6  | 4 7 8 1 1 1 3 4 5 5 8 9
8  | 1 3 0 0 4 5 6 7
10 | 1 6 6 6 8 8 9 9 9 9 0 3 5 5 5 5 8
12 | 1 4 5 7 1 1 3 8 8
14 | 6 2

10.6  10.9   13.3   11.5   11.5    9.0    7.1   10.8   13.1
 8.1  14.6    9.4   12.1    7.1    7.3    6.8   13.1   10.8
13.8   9.6   11.5    6.7    7.8    9.7    9.5    7.5   10.1
12.7  12.5    7.1   10.9   10.6   12.4   10.6    9.0    7.5
11.5   7.4   11.3   11.8    6.4    2.3   15.2    5.4   10.9
8.3   10.9    7.9   13.8   11.0

\(\sum_{i=1}^{50} x_i = 500.7\)
\(\sum_{i=1}^{50} x_i^2 = 5869.69\)
\(\sum_{i=1}^{50} (x_i - \bar{x})^2 = 336.4\)

La auditoría de la universidad desea conocer si el Centro Informático está cumpliendo con lineamientos establecidos por las normas para este tipo de servicios, dentro de los cuales se destacan:

No poseer datos atípicos.
No exceder las 10 horas para la atención. Solo está permitido un 5% de la muestra analizada.
Tener un 80% de los tiempos por debajo de las 8 horas (que equivalen a un día laboral).
Tener una distribución con asimetría positiva.

El responsable de la auditoría le pide revise cada uno de los lineamientos y su cumplimiento y realizar un breve informe.

Módulo 1

dgonzalez

Problemas

NOTA

Supermercados de ventas de alimentos:

Información