
Introducción
La regresión lineal es una de las herramientas fundamentales de la estadística aplicada y la ciencia de datos.
Permite estimar el valor promedio de una variable dependiente (respuesta) a partir de una o más variables independientes (predictoras) y medir el efecto que tienen los cambios en dichas variables explicativas sobre la respuesta.
Origen histórico del modelo
El origen formal del modelo de regresión lineal está ligado al desarrollo del método de los mínimos cuadrados a comienzos del siglo XIX.
Este método fue propuesto de manera independiente por:

- Adrien-Marie Legendre [1] en 1805, quien lo publicó en su obra Nouvelles méthodes pour la détermination des orbites des comètes como una técnica para ajustar órbitas de cuerpos celestes.
- Carl Friedrich Gauss[2], quien afirmó haber utilizado el método desde 1795 y lo publicó en 1809 en su libro Theoria motus corporum coelestium.
Ambos buscaban encontrar la “mejor recta” que se ajustara a un conjunto de puntos observados, minimizando la suma de los cuadrados de los errores.
Posteriormente, en la segunda mitad del siglo XIX, Francis Galton introdujo el término “regresión” al estudiar la relación entre la estatura de los padres y de los hijos. Al observar que las estaturas extremas (muy altas o muy bajas) tendían a acercarse al promedio en la siguiente generación, habló de “regresión hacia la media”. Más tarde, Karl Pearson y otros estadísticos formalizaron el procedimiento y lo extendieron a múltiples variables.
El desarrollo posterior de la teoría de regresión y correlación se consolidó con el trabajo de Karl Pearson y otros estadísticos de finales del siglo XIX y comienzos del XX.
Modelo de regresión lineal
\[Y_i = \beta_{0} + \beta_{1} X_{1} + \beta_{2} X_{2} + \beta_{3} X_{3} + ...... + \beta_{k} X_{k} + u \] donde :
\(Y\) : variable dependiente \(X_i\) : variables independientes \(\beta_{i}\) : coeficientes a estimar \(u\) : error aleatório
Ejemplo :
Supongamos que tenemos los datos correspondientes al ingreso de una persona (variable independiente) y su consumo (variable dependiente), para estimar el modelo siguimos los pasos:
- Construcción del diagrama de dispersión.
- Determinación de la forma funcional.
- Establecimiento de signos a priori.
- Estimación de los coeficientes.
- Comprobación de supuestos del modelo.
- Uso del modelo para pronóstico e interpretación.
En este caso (dos variables) tenemos un modelo de regresión lineal simple permite en el cual requerimos estimar el comportamiento de una variable respuesta \(Y\) a partir de una única variable explicativa \(X\):
\[Y_i = \beta_{0} + \beta_{1} X_{1} + u \]
donde:
- \(Y_i\): Variable dependiente
(respuesta) para el individuo \(i\) -
consumo.
- \(X_i\): Variable independiente
(predictora) para el individuo \(i\) -
ingreso.
- \(\beta_0\): Intercepto (valor
medio de \(Y\) cuando \(X = 0\)) - consumo
autónomo.
- \(\beta_1\): Pendiente (cambio
promedio en \(Y\) cuando \(X\) aumenta en una unidad).
- \(u_i\): Término de error (factores no observados, aleatorios).
En el contexto de este ejemplo:
- \(Y_i\) será el
Consumo.
- \(X_i\) será el Ingreso.
El método de Mínimos Cuadrados Ordinarios (MCO) busca encontrar los coeficientes de la linea recta \(\widehat{\beta}_0\) y \(\widehat{\beta}_1\) que minimicen la suma de los cuadrados de los residuos:
\[\sum_{i=1}^n (Y_i - \hat{Y}_i)^2 = \sum_{i=1}^n (Y_i - \hat{\beta}_0 - \hat{\beta}_1 X_i)^2\]
Supuestos del modelo de regresión lineal
En la formulación clásica se consideran, entre otros, los siguientes supuestos:
- Linealidad en los parámetros**: el modelo es lineal en \(beta_0\), \(\beta_1\).
- Valores de \(X\) fijos en muestreo
repetido** (o independientes del error).
- Modelo completo**: \(E[u_i \mid X] =
0\).
- Homoscedasticidad**: \(Var[u_i \mid X] =
\sigma^2\) (varianza constante).
- No autocorrelación**: \(Cov[u_i, u_j \mid
X] = 0\) para \(i \neq
j\).
- No multicolinealidad perfecta** (aplica más claramente en modelos
múltiples).
- Normalidad de los errores**: \(u_i \sim
N(0, \sigma^2)\).
- Exogeneidad**: \(E[u_i \mid X_i] =
0\).
- Existencia de variabilidad en X**: \(Var[X] > 0\).
- Número de observaciones suficiente**: \(n
\gg k\) (más observaciones que parámetros).
- Modelo correctamente especificado** (sin omisión importante de variables relevantes ni inclusión de términos incorrectos).
Los siguientes datos corresponden a 12 consumidores, para los cuales se midió su ingreso y consumo:
# Datos de ejemplo (Ingreso y Consumo)
Ingreso <- c(24.3, 12.5, 31.2, 28.0, 35.1, 10.5, 23.2, 10.0, 8.5, 15.9, 14.7, 15.0)
Consumo <- c(16.2, 8.5, 15.0, 17.0, 24.2, 11.2, 15.0, 7.1, 3.5, 11.5, 10.7, 9.2)
datos <- data.frame(
Consumidor = 1:12,
Ingreso = Ingreso,
Consumo = Consumo
)Ingreso <- c(24.3, 12.5, 31.2, 28.0, 35.1, 10.5, 23.2, 10.0, 8.5, 15.9, 14.7, 15.0) Consumo <- c(16.2, 8.5, 15.0, 17.0, 24.2, 11.2, 15.0, 7.1, 3.5, 11.5, 10.7, 9.2)
Diagrama de dispersión
El primer paso es construir el diagrama de dispersión para visualizar la relación entre ingreso y consumo.
library(ggplot2)
ggplot(datos, aes(x = Ingreso, y = Consumo)) +
geom_point(size = 3) +
geom_smooth(method = "lm", se = FALSE) +
labs(
title = "Consumo vs Ingreso",
x = "Ingreso",
y = "Consumo"
)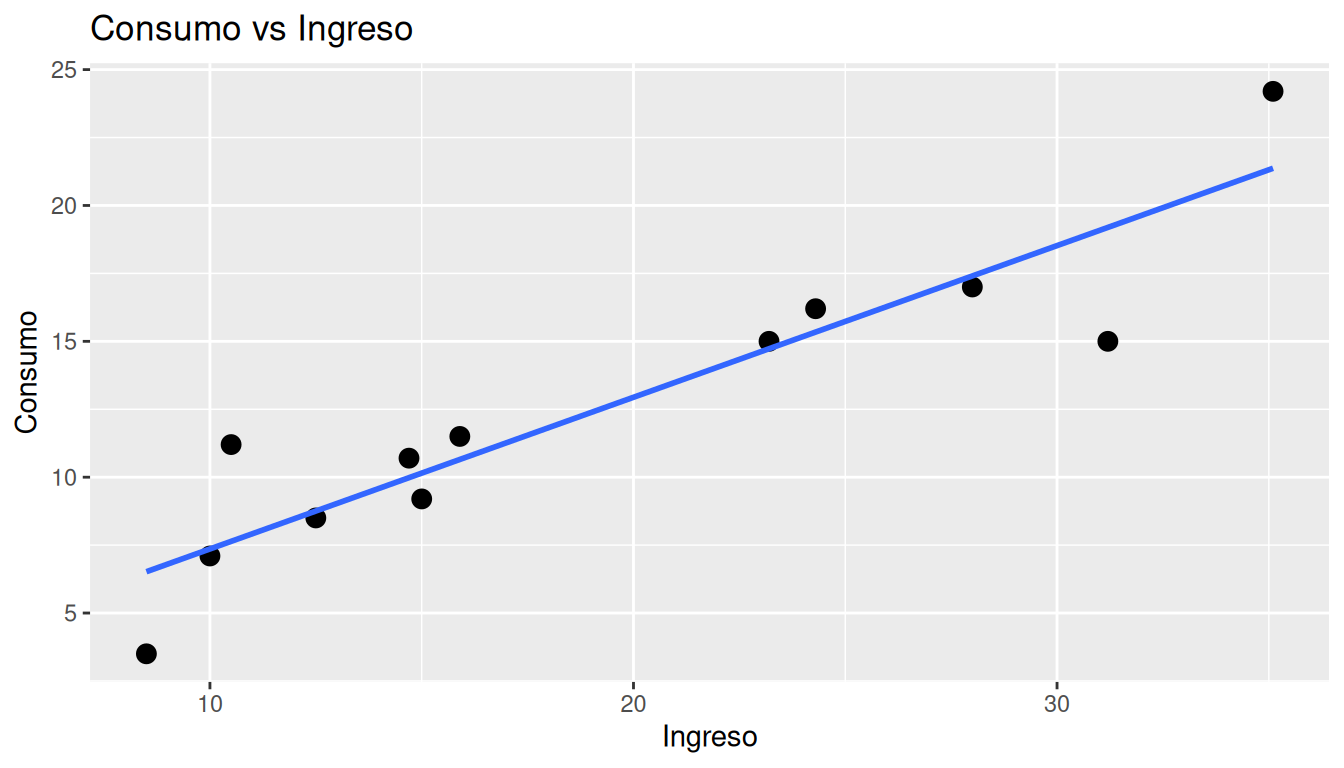
- Se observa una relación positiva: a mayores niveles
de ingreso, el consumo tiende a ser mayor.
- La nube de puntos sugiere que una relación lineal puede ser razonable como primera aproximación.
Signos a priori
Desde la teoría económica, si el bien es normal, se espera que:
- Cuando el ingreso aumenta, el consumo
también aumente.
- Por tanto, el parámetro \(\beta_1\)
(pendiente) debería ser positivo.
- El intercepto \(\beta_0\) puede ser positivo o negativo, pero su interpretación solo tiene sentido dentro del rango observado de los datos.
Estimación MCO
A continuación se ajusta el modelo:
\[\text{Consumo }_i = \beta_0 + \beta_1 \text{ Ingreso }_i + u_i\]
usando la función lm() de R.
modelo <- lm(Consumo ~ Ingreso, data = datos)
summary(modelo)
Call:
lm(formula = Consumo ~ Ingreso, data = datos)
Residuals:
Min 1Q Median 3Q Max
-4.1928 -0.5426 0.0088 0.8500 3.5613
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.77788 1.58292 1.123 0.288
Ingreso 0.55817 0.07567 7.376 2.38e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.251 on 10 degrees of freedom
Multiple R-squared: 0.8447, Adjusted R-squared: 0.8292
F-statistic: 54.41 on 1 and 10 DF, p-value: 2.38e-05La salida de summary(modelo) incluye:
- Los estimadores o coeficientes estimados :\(\widehat{\beta}_0\) y \(\widehat{\beta}_1\).
- Sus errores estándar, valores t y p-valores.
- El coeficiente de determinación \(R^2\) y el \(R^2\) ajustado.
- La estimación de la varianza residual \(\widehat{\sigma}^2\).
Interpretación de los coeficientes
- \(\hat{\beta}_0\): Consumo promedio
cuando el ingreso es 0, o consumo autónomo.
- \(\hat{\beta}_1\): Incremento promedio en el consumo por cada unidad adicional de ingreso.
Evaluación de supuestos
En este caso nos concetraremos en los suspuestos sobre los errores \(u\). Para ello emplearemos los residuales \(\widehat{u} = y_i - \widehat{y}_{i}\)
# Cálculo de residuos y valores ajustados
residuos <- resid(modelo)
ajustados <- fitted(modelo)
datos_diag <- data.frame(
Ingreso = datos$Ingreso,
Consumo = datos$Consumo,
Ajustado = ajustados,
Residuo = residuos
)
head(datos_diag) Ingreso Consumo Ajustado Residuo
1 24.3 16.2 15.341446 0.8585544
2 12.5 8.5 8.755023 -0.2550230
3 31.2 15.0 19.192828 -4.1928284
4 28.0 17.0 17.406680 -0.4066799
5 35.1 24.2 21.369697 2.8303031
6 10.5 11.2 7.638680 3.5613199S1. Linealidad y especificación del modelo
Se analiza el gráfico de residuos vs valores ajustados. Si la relación es lineal, no debería observarse patrón sistemático.
ggplot(datos_diag, aes(x = Ingreso, y = Consumo)) +
geom_point(size = 2) +
geom_hline(yintercept = 0, linetype = "dashed") +
labs(
title = " ",
x = "Ingreso",
y = "Consumo"
)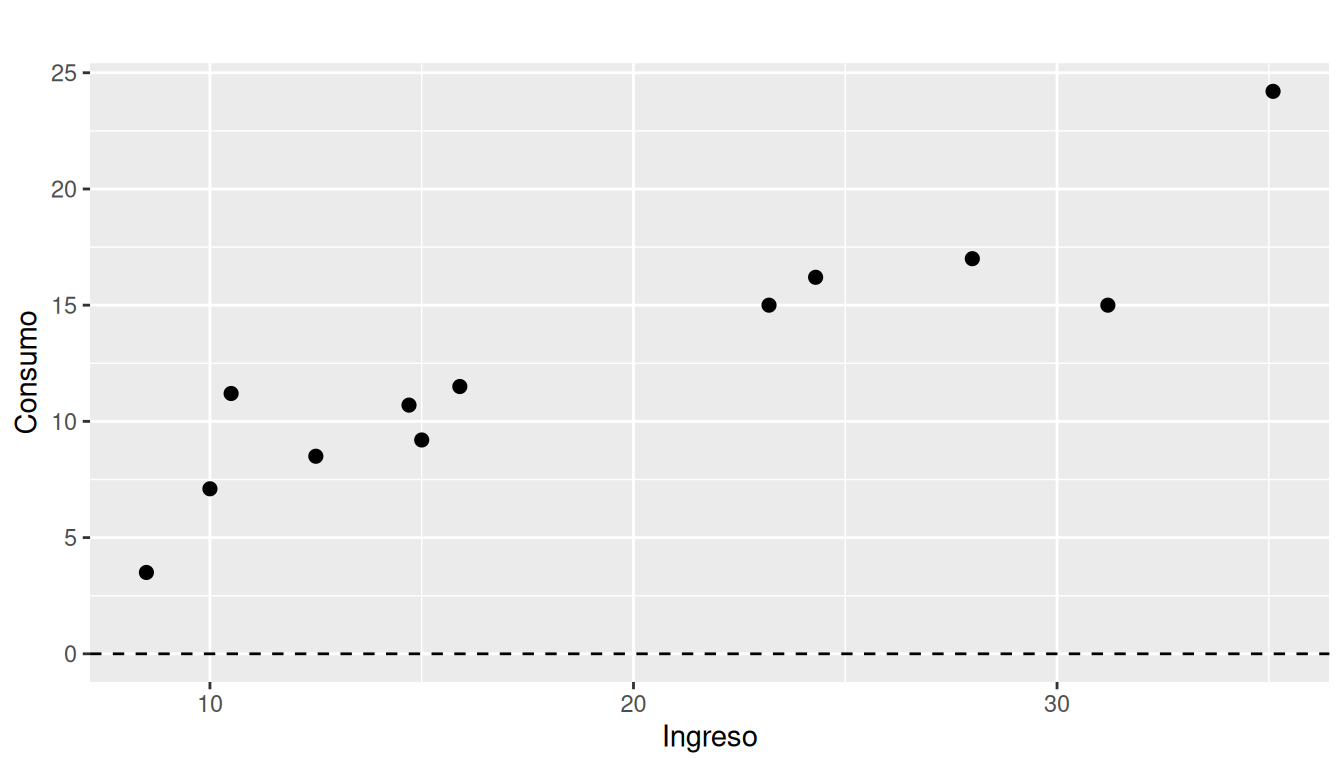
Comentar aquí si se observa algún patrón (curvatura, forma de linea recta , etc.).
S2. Homoscedasticidad (varianza constante)
ggplot(datos_diag, aes(x = Ajustado, y = Residuo)) +
geom_point(size = 2) +
geom_hline(yintercept = 0, linetype = "dashed") +
labs(
title = " ",
x = "Consumo ajustado",
y = "Residuos"
)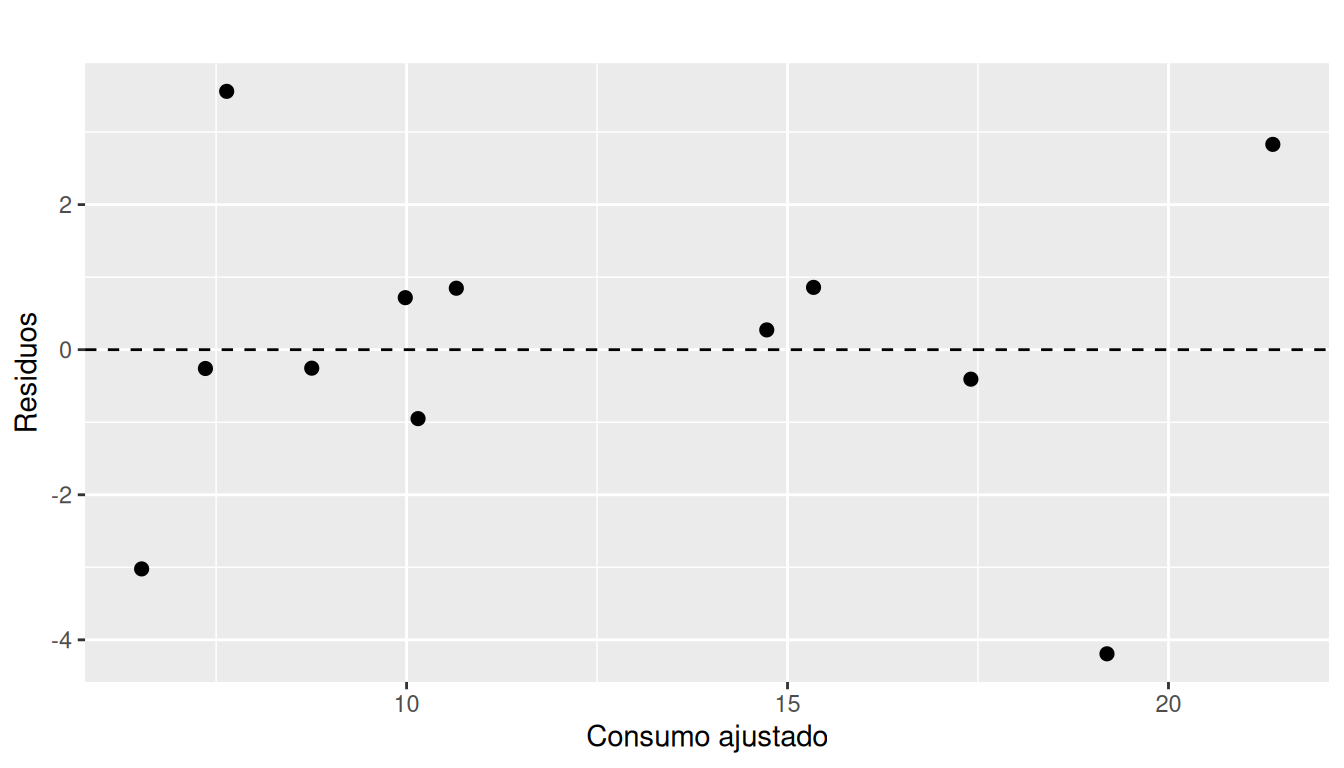
Si la dispersión de los residuos alrededor de 0 es más o menos constante, se apoya la hipótesis de homoscedasticidad.
Prueba de White (vía Breusch-Pagan extendida)
Utilizamos la prueba de Breusch-Pagan (bptest) con una
especificación que incluye el valor ajustado y su cuadrado, estilo
prueba de White.
library(lmtest)
# Prueba tipo White: u^2 ~ Ajustado + Ajustado^2
bptest(modelo, ~ Ajustado + I(Ajustado^2), data = datos_diag)
studentized Breusch-Pagan test
data: modelo
BP = 4.6547, df = 2, p-value = 0.09755- Hipótesis nula (Ho): Homoscedasticidad (varianza
constante).
- Hipótesis alterna (Ha): Heteroscedasticidad (varianza no constante).
Si el p-valor es mayor que un nivel de significancia (\(\alpha =0.05\)), no se rechaza la homoscedasticidad.
S3. Normalidad de los errores
Histograma de residuos
ggplot(datos_diag, aes(x = Residuo)) +
geom_histogram(bins = 5) +
labs(
title = "Histograma de residuos",
x = "Residuo",
y = "Frecuencia"
)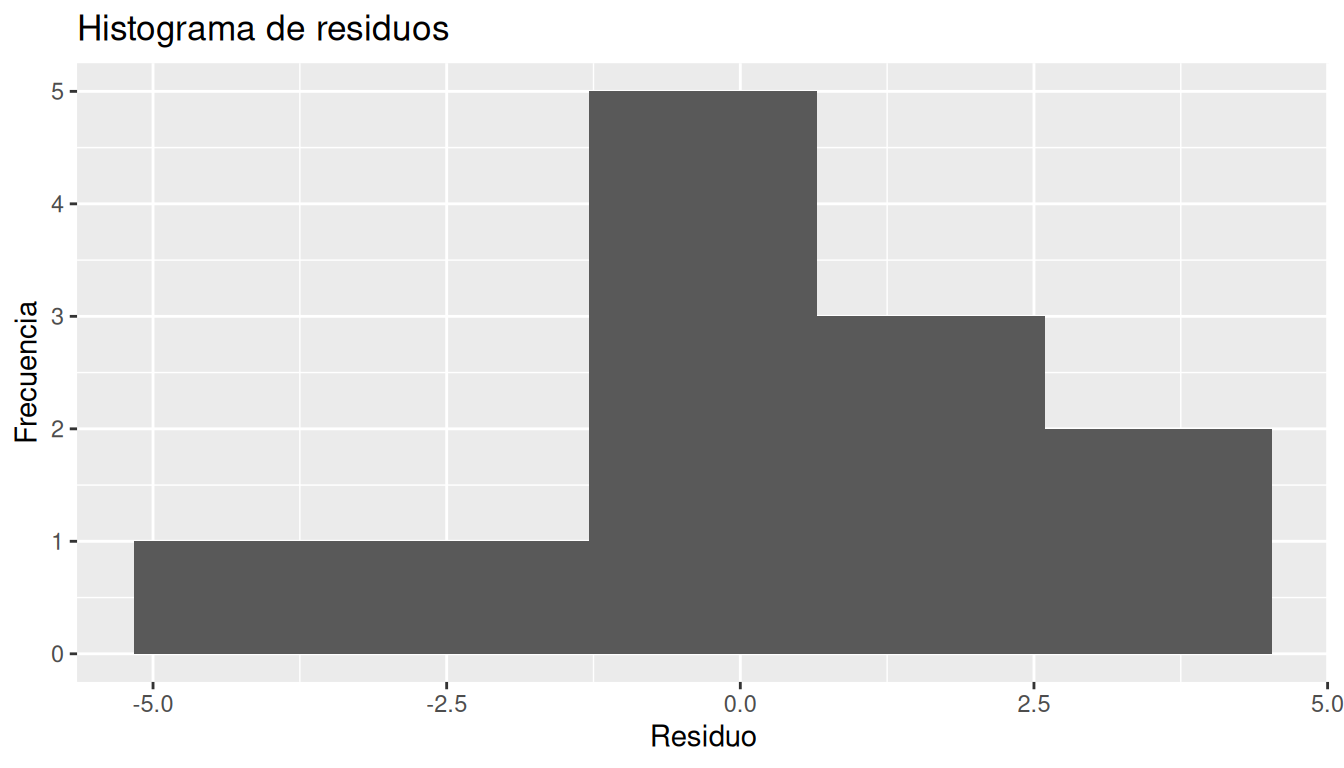
Gráfico Q-Q (probabilidad normal)
qqnorm(residuos)
qqline(residuos, col = "red")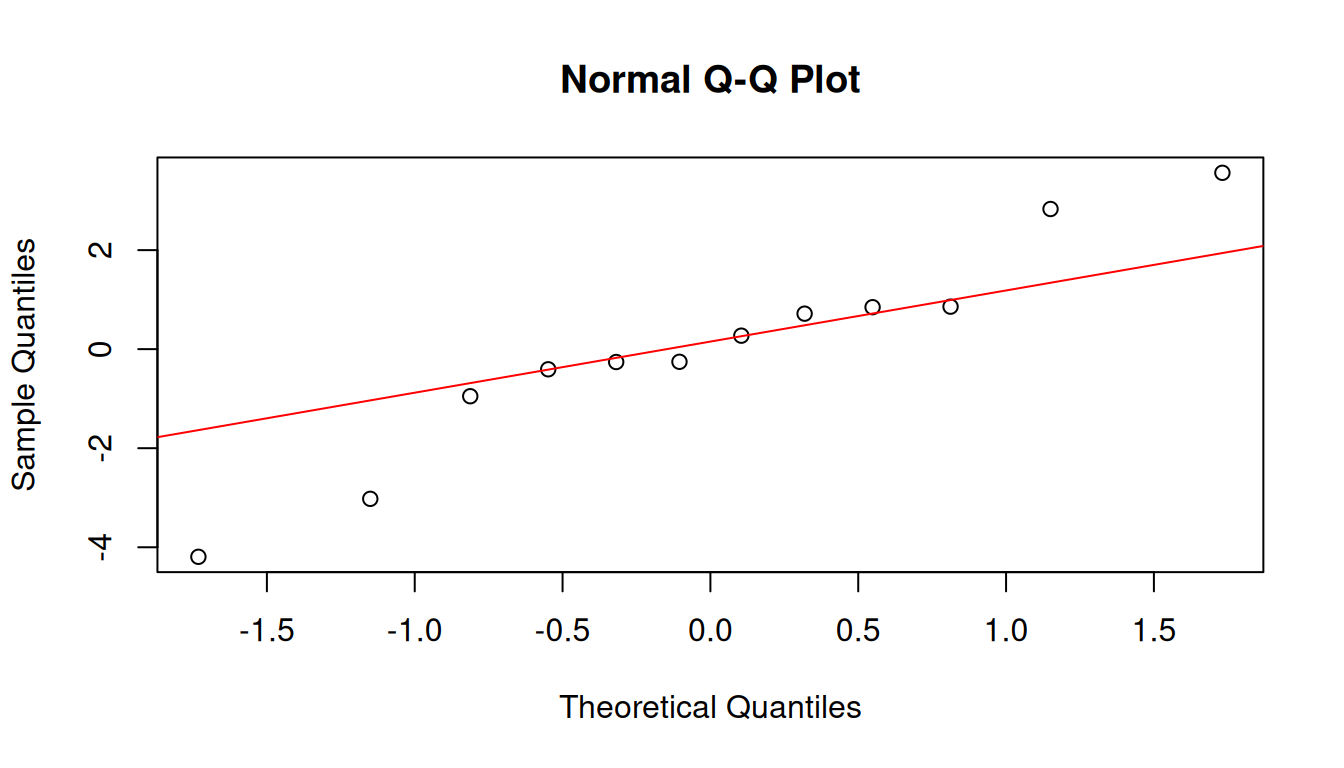
Si los puntos siguen aproximadamente la línea recta, los residuos pueden considerarse aproximadamente normales.
Prueba de Kolmogorov-Smirnov y Shapiro-Wilk
# K-S test comparando con normal N(media, sd) de los residuos
ks.test(
residuos,
"pnorm",
mean = mean(residuos),
sd = sd(residuos)
)
Exact one-sample Kolmogorov-Smirnov test
data: residuos
D = 0.17788, p-value = 0.7814
alternative hypothesis: two-sided# Prueba de Shapiro-Wilk (recomendada para n pequeño)
shapiro.test(residuos)
Shapiro-Wilk normality test
data: residuos
W = 0.94569, p-value = 0.5751- En ambas pruebas, la H0 es que los residuos provienen de una
distribución normal.
- Un p-valor alto (mayor a \(\alpha=0.05\)) indica que no se rechaza la normalidad.
S4. No autocorrelación de los errores (Durbin-Watson)
Aunque el ejemplo es de datos de corte transversal y no de series de tiempo, se ilustra la prueba de Durbin-Watson.
# Prueba de Durbin-Watson
dwtest(modelo)
Durbin-Watson test
data: modelo
DW = 1.5517, p-value = 0.1769
alternative hypothesis: true autocorrelation is greater than 0- H0: No hay autocorrelación de primer orden en los
errores.
- Un p-valor grande sugiere que no hay evidencia fuerte de autocorrelación.
En datos de corte transversal, usualmente este supuesto se considera razonable a menos que haya un ordenamiento natural que genere correlación (por ejemplo, geográfico o por grupos).
Otros supuestos
No multicolinealidad: en el modelo simple solo hay una \(X\), por lo que no hay multicolinealidad entre variables explicativas.
Exogeneidad: es un supuesto más teórico. Implica que factores no observados que afectan al consumo no están correlacionados con el ingreso (por ejemplo, preferencias, educación, etc.).
Correcta especificación: se requiere juzgar si falta alguna variable importante (como tamaño del hogar, edad, etc.) o alguna forma funcional no lineal.
Uso del modelo
Una de las aplicaciones principales del modelo de regresión es predecir el consumo dado un nivel de ingreso y construir intervalos de confianza para la respuesta media y para una observación individual.
Pronóstico puntual
Por ejemplo, supongamos que deseamos predecir el consumo para los siguientes niveles de ingreso: 15, 20 y 30 unidades.
nuevos_datos <- data.frame(
Ingreso = c(15, 20, 30)
)
predicciones <- predict(modelo, newdata = nuevos_datos)
cbind(nuevos_datos, Consumo_Pronosticado = predicciones) Ingreso Consumo_Pronosticado
1 15 10.15045
2 20 12.94131
3 30 18.52302Intervalo de confianza para el valor medio de consumo
pred_media <- predict(
modelo,
newdata = nuevos_datos,
interval = "confidence",
level = 0.95 # 95% de confianza
)
cbind(nuevos_datos, pred_media) Ingreso fit lwr upr
1 15 10.15045 8.548063 11.75284
2 20 12.94131 11.485322 14.39730
3 30 18.52302 16.180228 20.86582- Estas bandas reflejan la incertidumbre en la estimación de la media de consumo para esos niveles de ingreso.
Intervalo de predicción para una observación individual
pred_pred <- predict(
modelo,
newdata = nuevos_datos,
interval = "prediction",
level = 0.95 # 95% de predicción
)
cbind(nuevos_datos, pred_pred) Ingreso fit lwr upr
1 15 10.15045 4.885993 15.41491
2 20 12.94131 7.719549 18.16307
3 30 18.52302 12.988083 24.05796- Estos intervalos son más amplios que los de confianza, porque incluyen la variabilidad del término de error individual.
Conclusiones
El análisis del modelo de regresión lineal simple comprende :
El diagrama de dispersión sugiere una relación positiva entre las variables \(X\) y \(Y\) .
La estimación del modelo por el método de Mínimos Cuadrados Ordinarios que proporciona un modelo de la forma:
\[\widehat{Y} = \widehat{\beta}_0 + \widehat{\beta}_1 X\]
con \(\hat{\beta}_1 > 0\), consistente con la teoría económica para un bien normal.
Los diagnósticos de residuos permiten evaluar:
- La adecuación de la forma lineal.
- La homoscedasticidad (prueba tipo White /
Breusch-Pagan).
- La normalidad de los errores (K-S y
Shapiro-Wilk).
- La ausencia de autocorrelación (Durbin-Watson, ilustrativo en este contexto).
- La adecuación de la forma lineal.
El modelo puede usarse para:
- Pronosticar el valor de \(Y\) dado un valor de \(X\).
- Calcular intervalos de confianza para el valor de
\(Y\) promedio.
- Calcular intervalos de predicción para nuevas observaciones de X, siempre y cuando se trate de una interpolación.
- Pronosticar el valor de \(Y\) dado un valor de \(X\).