FUNCIÓN EXPONENCIAL

La función exponencial es una función matemática fundamental en la que el valor de la función crece (o decrece) rápidamente a medida que el valor de la variable independiente aumenta. La forma general de la función exponencial es :

Definición

\[ f(x) = a . b ^{x} \]

Donde :

• \(a\) : Es un parámetro que representa el valor inicial de la función cuando \(x=0\). Es la ordenada al origen o el valor de la función cuando \(x=0\).

• \(b\) : Es la base de la función exponencial. Determina la tasa de crecimiento de la función.

  • Si \(b>1\), la función crece exponencialmente.
  • Si \(0<b<1\), la función decrece exponencialmente.

• \(x\) : Es la variable independiente. Representa el valor que se evalua para obtener el valor de \(f(x)\).

Propiedades

• \(b^x . b^y = b^{x+y}\)
• \(\dfrac{b^x}{b^y} = b^{x-y}\)
• \((b^x)^y = b^{xy}\)
• \(b^{x+y} \neq b^x + b^y\)
• \(b^0 = 1\)
• \(b^1 = b\)

Un caso particular ocurre cuando \(b = e\)

Caso f(x) = exp{x}

library(ggplot2)

# Datos
x <- seq(-2, 2, by = 0.1)
y <- exp(x)
data <- data.frame(x = x, y = y)

# Gráfico
ggplot(data, aes(x = x, y = y)) +
  geom_line(color = "darkblue") +
  labs(title = "Gráfico de la función exponencial f(x) = exp{x}",
       x = "x",
       y = "y") +
  theme_minimal()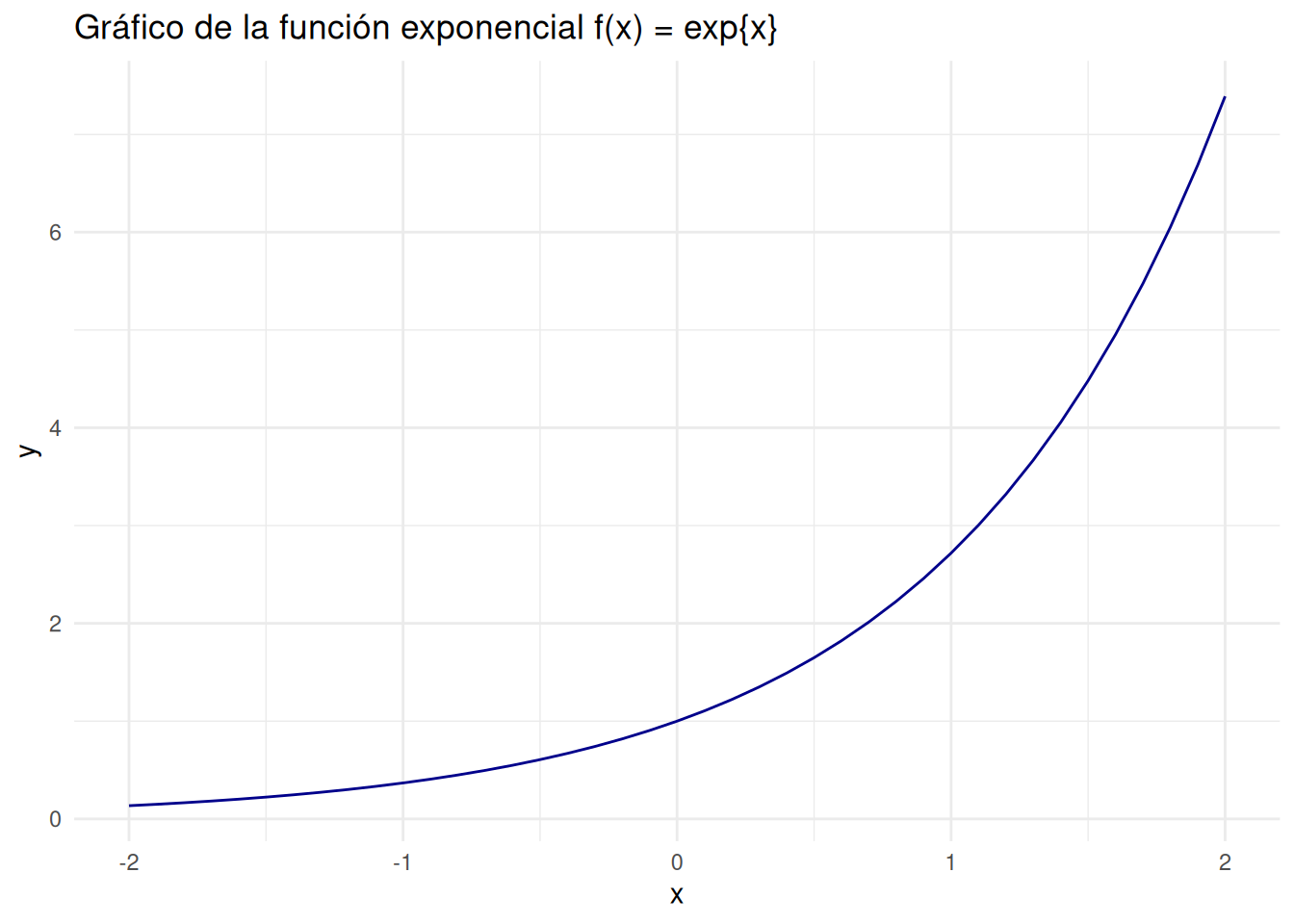

Caso f(x) = exp{-x}

library(ggplot2)

# Datos
x <- seq(-2, 2, by = 0.1)
y <- exp(-x)
data <- data.frame(x = x, y = y)

# Gráfico
ggplot(data, aes(x = x, y = y)) +
  geom_line(color = "darkblue") +
  labs(title = "Gráfico de la función exponencial  f(x) = exp{-x}",
       x = "x",
       y = "y") +
  theme_minimal()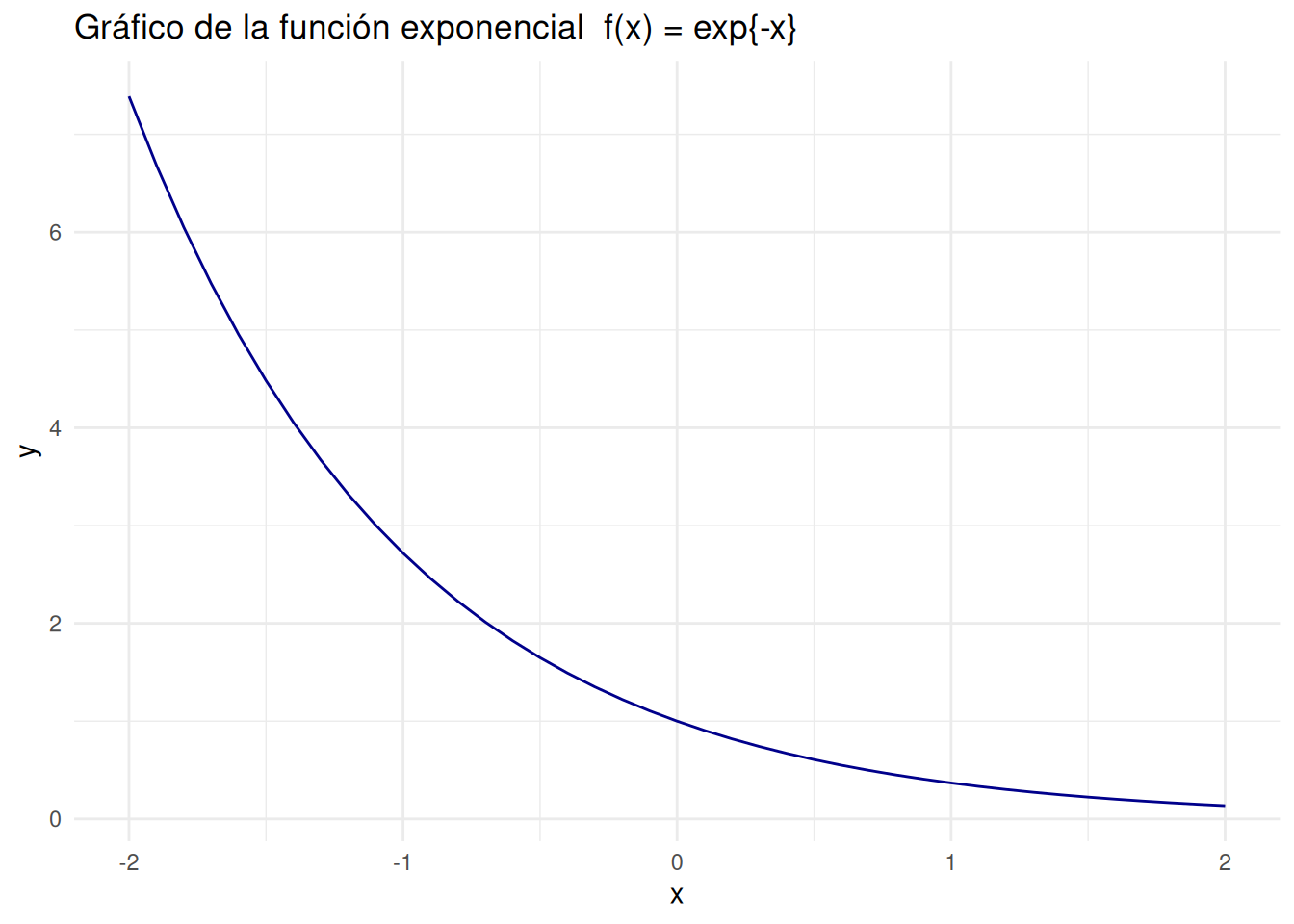

Una de las funciones de densidad de probabilidad más conocida en estadística es el modelo exponencial

\[f(x) = \dfrac{1}{\lambda} \hspace{.2cm} exp{(-1/\lambda)}\]

Para un valor de \(\lambda = 2\) tenemos la siguiente función:

\[f(x) = \dfrac{1}{2} \hspace{.2cm} exp{(-x/2)}, \hspace{1cm} x>0\]

library(ggplot2)

# Datos
x <- seq(0, 6, by = 0.1)
y <- 1/2*exp(-x/2)
data <- data.frame(x = x, y = y)

# Gráfico
ggplot(data, aes(x = x, y = y)) +
  geom_line(color = "darkblue") +
  labs(title = "Gráfico de la función exponencial  f(x) = exp{-x}",
       x = "x",
       y = "y") +
  theme_minimal()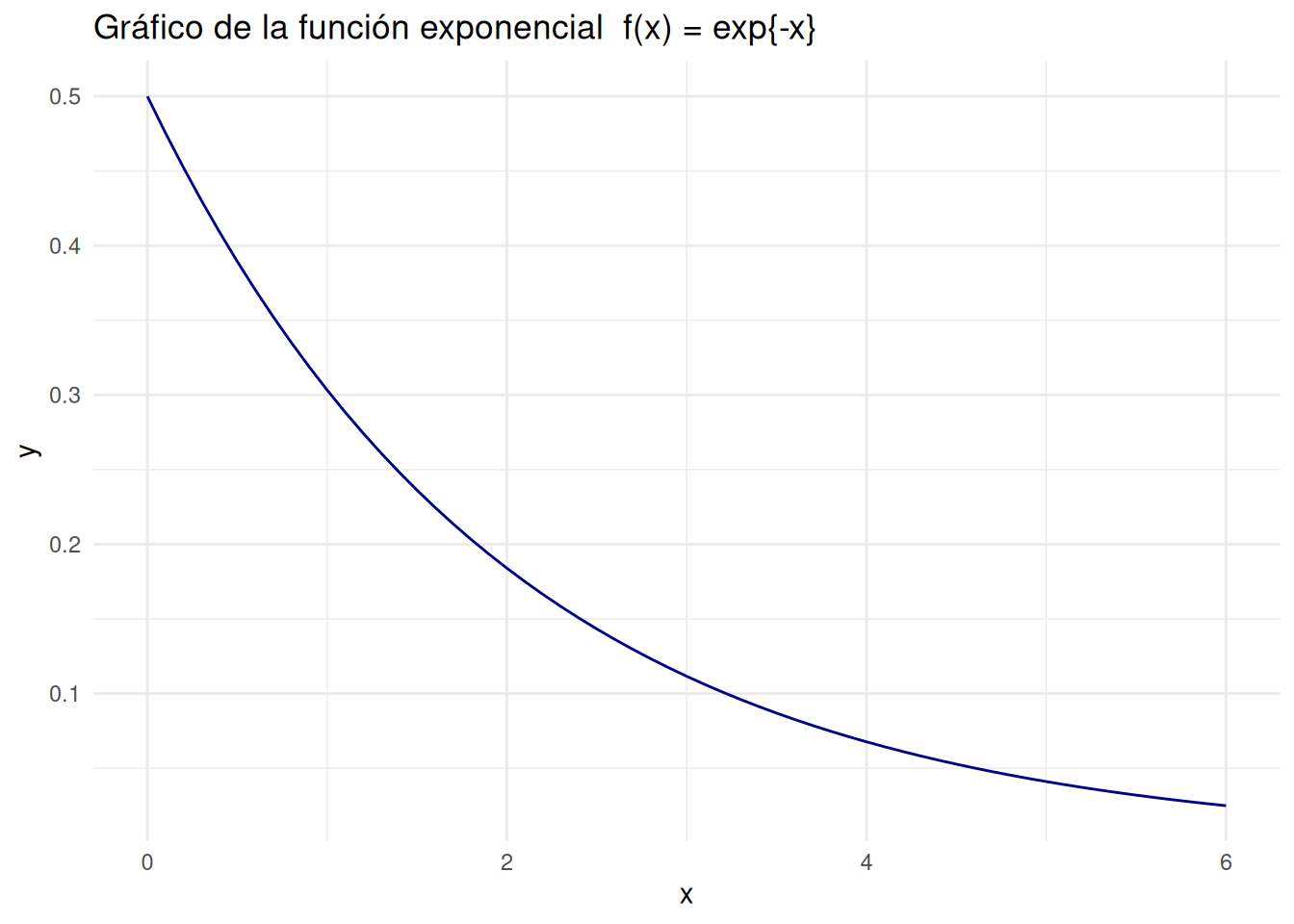

Problemas propuestos

1. Dado un valor inicial de \(a = 2\) y una tasa de crecimiento \(b = 1.5\), escribe la función exponencial correspondiente y calcula el valor de \(f(x)\) cuando \(x = 3\). ¿Cómo cambia el valor de \(f(x)\) si \(b\) es mayor o menor a 1?

2. Verifica la propiedad \(b^x \cdot b^y = b^{x+y}\) usando \(b = 2\), \(x = 3\) y \(y = 4\). Escribe la ecuación y demuestra que ambos lados son iguales.

3. Considera la función exponencial \(f(x) = 3 \cdot (0.5)^x\). Grafica la función y analiza cómo cambia el valor de \(f(x)\) a medida que \(x\) aumenta. ¿Qué sucede cuando \(x\) es negativo?

4. Compara las funciones \(f(x) = 2^x\) y \(g(x) = 3^x\). Grafica ambas funciones en el mismo plano y determina para qué valores de \(x\) \(f(x)\) es mayor que \(g(x)\).

5. Considera la función de densidad de probabilidad exponencial \(f(x) = \frac{1}{2} \cdot \exp{\left(-\frac{x}{2}\right)}\), donde \(\lambda = 2\). Calcula la probabilidad de que \(x\) sea menor que 2 utilizando la función de distribución acumulativa correspondiente.