
Experimentos aleatorios
Como se menciona en la Guía 2.1, un Experimento aleatorio se puede definir como una acción que podemos repetir en iguales condiciones muchas veces y cuyo resultado no conocemos anticipadamente
Un ejemplo de ello es cuando estamos jugando parques y un jugador lanza dos dados, el resultado solo es posible de observar después de haber realizado la acción de lanzarlos.
Al conjunto de todos los posibles valores que puede tomar el experimento aleatorio se le denomina Espacio muestral, que se denota por la letra mayuscula S.

Para este ejemplo :
\[S=\{ 2,3,4,5,6,7,8,9,10,11,12
\}\]
Lanzamiento de un dados
Para simular el lanzamiento de un dado utilizaremos la función
sample(x, size, replace = FALSE, prob = NULL), con
parámetros: x : valores del espacio muestral;
size : tamaño de la muestra y replace : para
determinar si la selección se realiza con remplazo o sin remplazo.
sample(1:6,200, replace = TRUE), da un resultado una
muestra de 200 valores enteros entre 1 y 6, con repetición.
n=200
x=sample(1:6,n, replace = TRUE)
td1=prop.table(table(x))
barplot(td1, las=1)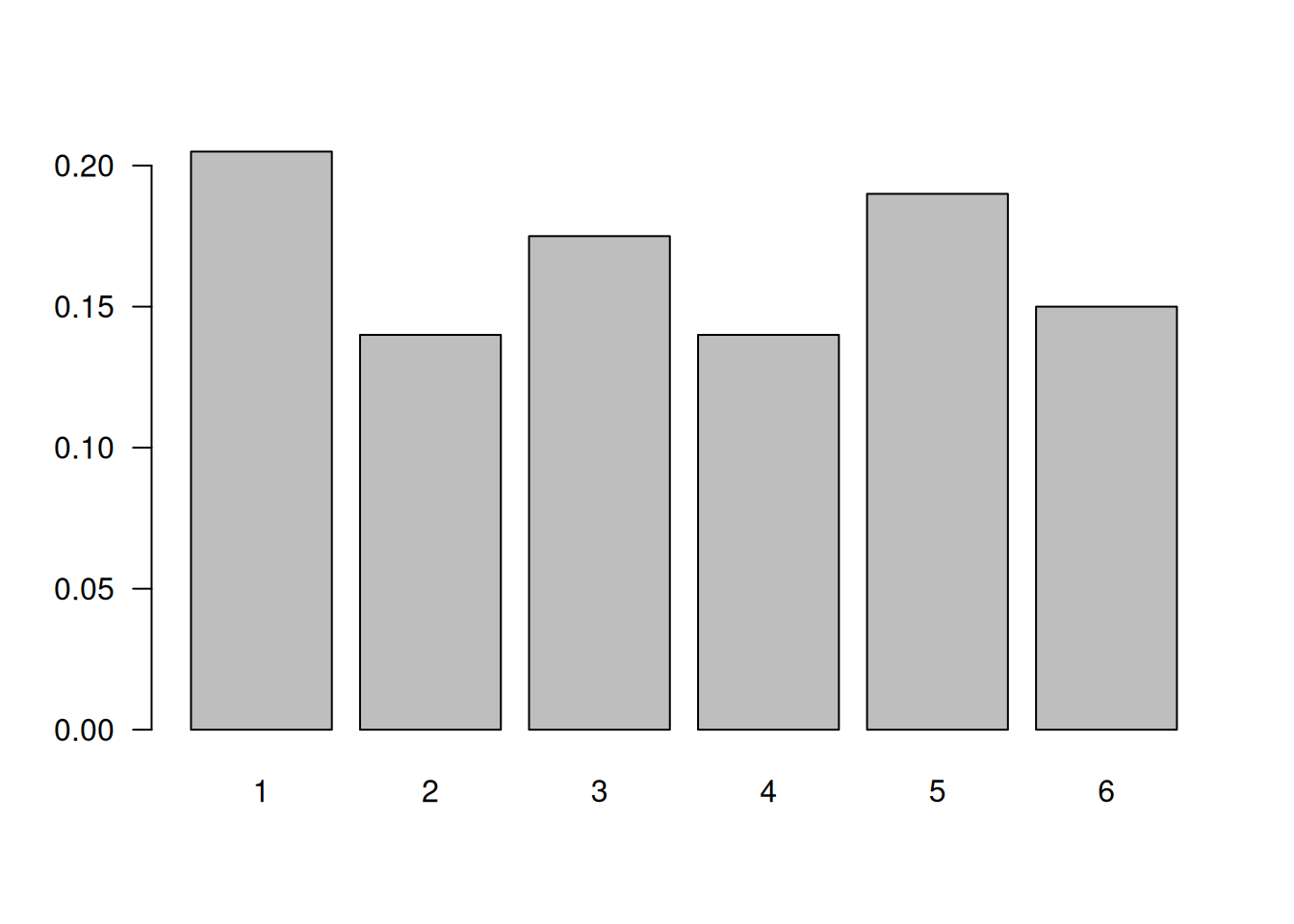
Lanzamiento de dos dados
En este caso utilizamos la función sample() dos veces y
se obtienen dos vectores que representan los resultados del dado1 y del
dado2 respectivamente. Con estos resultados se construye una
data.frame() de dos columnas por n filas. En ella cada fila
de dos componentes conforma una muestra con dos valores.
Para obtener la suma de los valores de los dos dados, utilizamos la
función apply(X, MARGIN, FUN, ..., simplify = TRUE)
indicando con MARGIN=1 que la operación (siguiente
parámetro) se realizará por filas. Por último en el parámetro
FUN se asigna la función a realizar. En resumen :
suma=apply(dados, 1, sum)
n=20000000
d1=sample(1:6,n, replace = TRUE)
d2=sample(1:6,n, replace = TRUE)
dados=data.frame(d1,d2)
suma=apply(dados, 1, sum)
barplot(table(suma), las=1,cex.axis=0.7)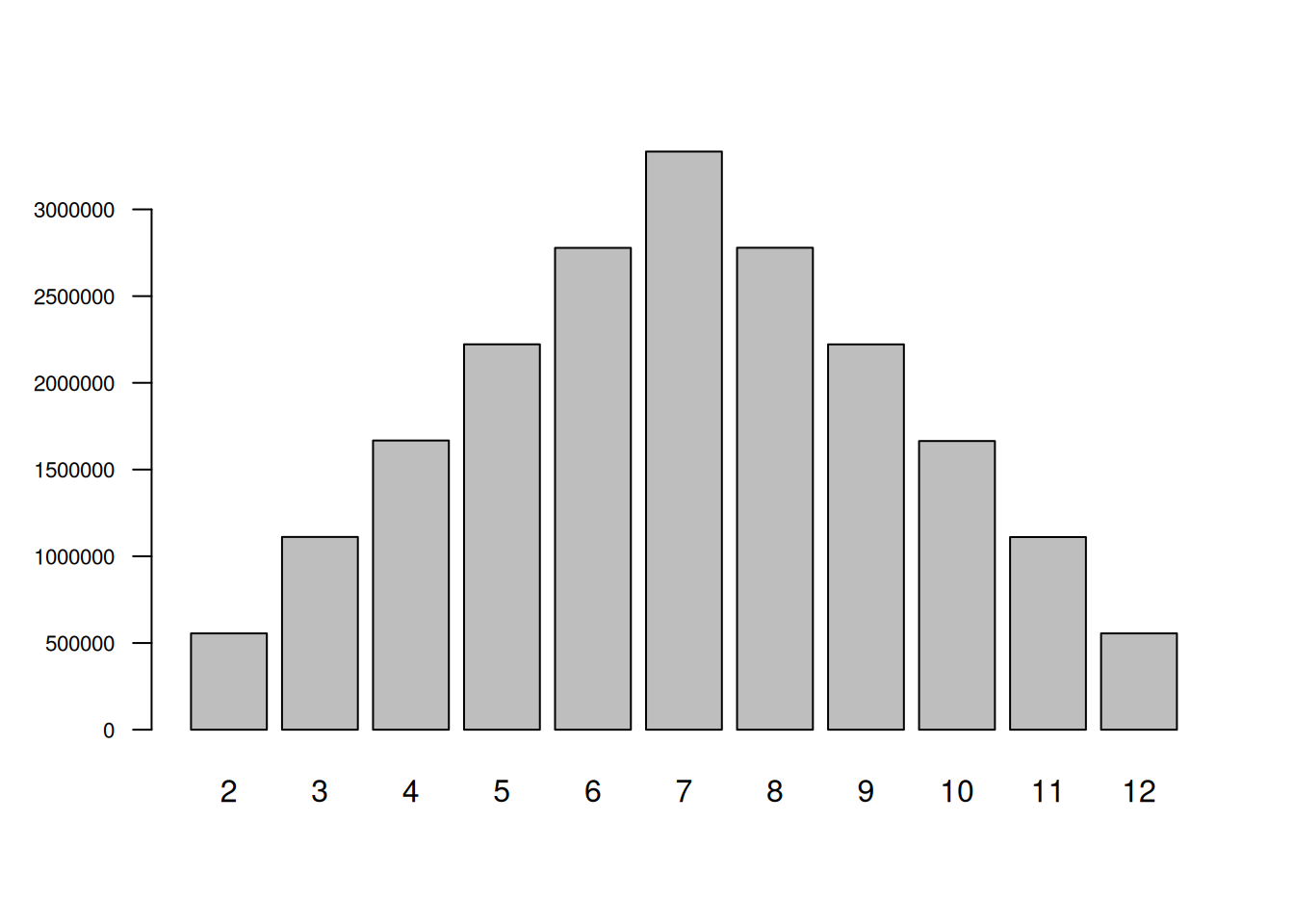
data.frame(prop.table(table(suma))) suma Freq
1 2 0.02777585
2 3 0.05557895
3 4 0.08338395
4 5 0.11110115
5 6 0.13890640
6 7 0.16667970
7 8 0.13894065
8 9 0.11109410
9 10 0.08322200
10 11 0.05553835
11 12 0.02777890Procedimiento alternativo
t=sapply(1:200, function(x){sum(sample(1:6,2,rep=T))})
barplot(table(t), las=1, cex.axis=0.7)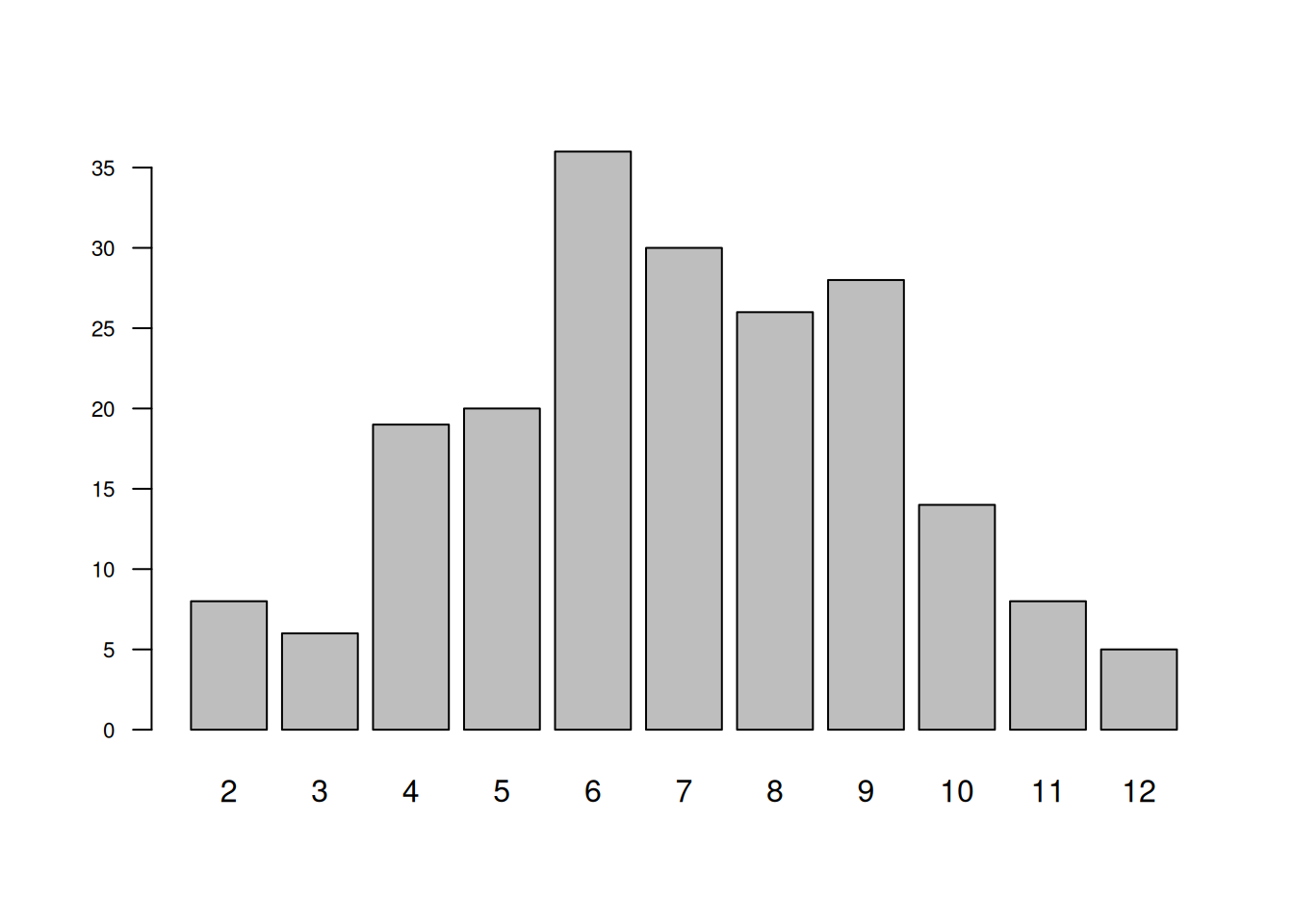
Urna
Para simular la extracción de bolas de una urna, se utilizan las
funciones sample() y rep() mostradas en el
siguiente ejemplo :
- Simulación de urna con: 3 bolas Blancas, 5 Rojas y 4 Azules
- 1 representa las bolas blancas
- 2 representa las bolas rojas
- 3 representa las bolas azules
sample(c(1,2,3),2,rep=T,prob=c(3,5,4))[1] 2 2La misma simulación con palabras
sample(c("Blanca","Roja","Azul"),2,rep=T,prob=c(3,5,4))[1] "Roja" "Blanca"Tablas de contingencia
Las tablas de contingencia o tablas cruzadas se basan en las tablas de frecuencia para dos variables cualitativas o cuantitativas con pocos valores. En ellas se representan probabilidades conjuntas, marginales y condicionales
Inicialmente construimos una tabla con los valores de las frecuencias relativas conjuntas
x=c(20,60,100,30,140,50)
m=matrix(x,ncol=2)
rownames(m)=c("Adminitrativo","Operativo","Vendedor")
colnames(m)=c("Mujer","Hombre")
m Mujer Hombre
Adminitrativo 20 30
Operativo 60 140
Vendedor 100 50En este caso se adicionan las frecuencias relativas marginales
addmargins(m) Mujer Hombre Sum
Adminitrativo 20 30 50
Operativo 60 140 200
Vendedor 100 50 150
Sum 180 220 400Para convertirlas en probabilidades utilizamos la función
prop.table()
prop.table(m) Mujer Hombre
Adminitrativo 0.05 0.075
Operativo 0.15 0.350
Vendedor 0.25 0.125Esta función también se utiliza para calcular las probabilidades condicionales por filas
prop.table(m,1) Mujer Hombre
Adminitrativo 0.4000000 0.6000000
Operativo 0.3000000 0.7000000
Vendedor 0.6666667 0.3333333o las probabilidades condicionales por columnas
prop.table(m,2) Mujer Hombre
Adminitrativo 0.1111111 0.1363636
Operativo 0.3333333 0.6363636
Vendedor 0.5555556 0.2272727Ubicación por estado contagiados de Covid en Colombia
# Colombia= readRDS("data/Colombia.RDS")
t21=table(Colombia23$ubicacion, Colombia23$estado)
(t22=addmargins(t21))
FALLECIDO GRAVE LEVE MODERADO N/A Sum
CASA 0 0 9162 0 0 9162
FALLECIDO 69 0 0 0 0 69
HOSPITAL 0 0 0 331 0 331
HOSPITAL UCI 0 33 0 0 0 33
N/A 0 0 0 0 41 41
Sum 69 33 9162 331 41 9636La tabla de frecuencias la convertimos en tabla de probabilidades
t23=prop.table(t21)
round(t23, 4)
FALLECIDO GRAVE LEVE MODERADO N/A
CASA 0.0000 0.0000 0.9508 0.0000 0.0000
FALLECIDO 0.0072 0.0000 0.0000 0.0000 0.0000
HOSPITAL 0.0000 0.0000 0.0000 0.0344 0.0000
HOSPITAL UCI 0.0000 0.0034 0.0000 0.0000 0.0000
N/A 0.0000 0.0000 0.0000 0.0000 0.0043En el módulo 3 se presentan otro tipo de simulaciones partiendo del supuesto de un modelo de probabilidad y del conocimiento de las probabilidades de algunos eventos