Conjuntos
Módulo 0
dgonzalez
Introducción
A continuación se relacionan las principales características de los conjuntos y sus principales relaciones. Estos conceptos serán importante en el momento de abordar los conceptos básicos de probabilidad que serán expuestos en el Modulo 2.
En pesaremos con su definición
Conjunto
Un conjunto es una colección de objetos que se denota con una letra mayúscula (comúnmente las primeras letras del alfabeto A,B,C..) .
Se pueden escribir por:
por extensión : \(A=\{0,1,2,3,4,5,6,7,8,9\}\), escribiendo todos los elementos que lo conforman.
por su nombre : los dígitos
por compresión : \(A=\{ x\in\mathbb{Z}, 0\le x \le 9 \}\), utilizando nomenclatura matemática.
Al comparar o combinar conjuntos debemos hacer uso de sus propiedades y operaciones, dentro de las cuales se encuentran \(A \cup B\), \(A \cap B\),
Unión del conjunto
Unión del \(A\) con el conjunto \(B\). \(A \cup B\), \(\overline{A}\) ,\(A - B\), entre otras. La zona sombreada en la siguiente figura representa estas operación
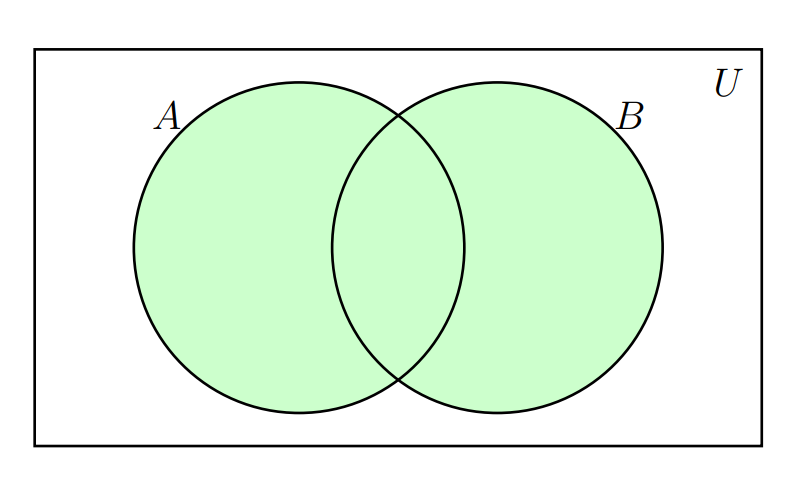
Supongamos los siguientes conjuntos
- \(A = \{a,e,i,o,u \}\) y
- \(B = \{1,2,3,4,5,6,7,8,9,0\}\)
\[A \cup B = \{a,e,i,o,u, 1,2,3,4,5,6,7,8,9,0 \}\]
Intersección
La intersección entre el conjunto \(A\) y el \(B\) se denota por : \(A \cap B\) y se representa por la siguiente zona sombreada
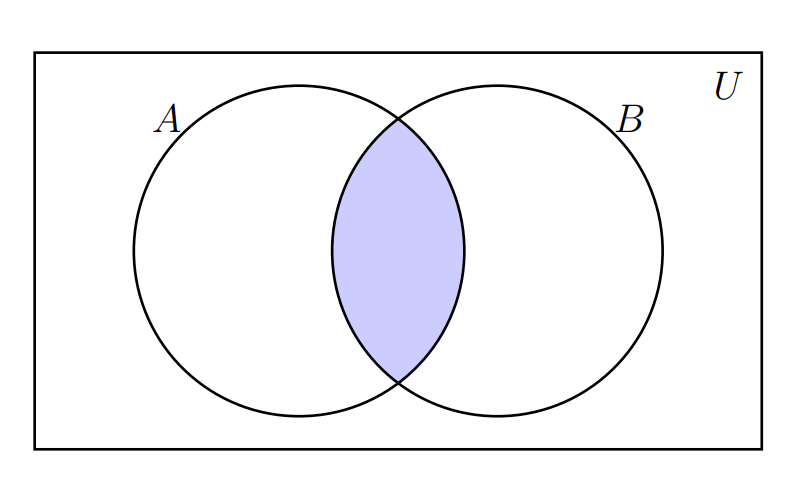
Supongamos los siguientes conjuntos:
- \(A = \{1,2,3,4,5,6 \}\) y
- \(B = \{2,4,6,8,10,12,14,16,18,20 \}\)
\[A \cap B = \{ 2,4,6 \}\]
Complemento
El complemento del conjunto \(A\) se escribe como: \(\overline{A}\) y se representa por la siguiente zona sombreada
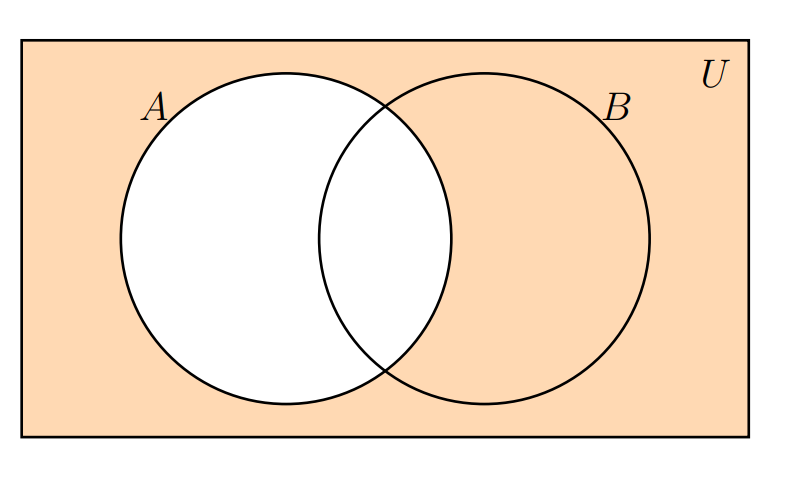
Supongamos los siguientes conjuntos:
- \(U = \{0, 1,2,3,4,5,6. 7, 8, 9\}\) y
- \(A = \{1,2,3,4,5,6 \}\) y
\[\overline{A} = \{0, 7, 8, 9 \}\]
Resta
La resta del conjunto \(B\) menos el conjunto \(A\) : \(B-A\) , está representada por la zona sombreada en la siguiente figura
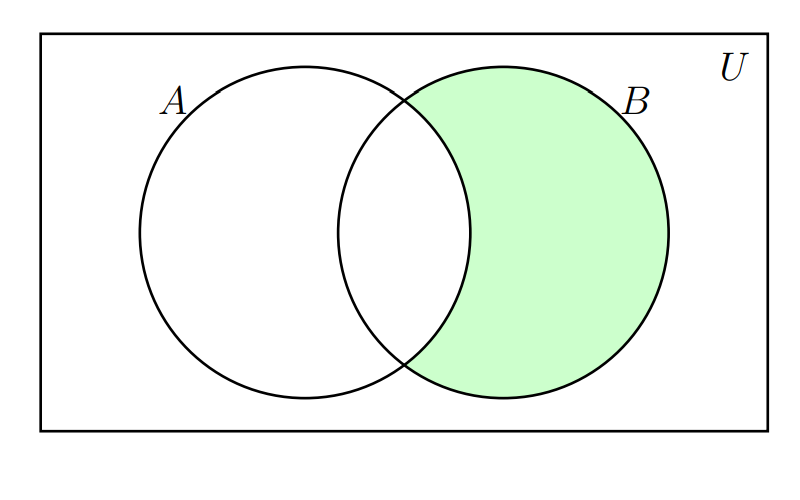
Supongamos los siguientes conjuntos
- \(A = \{1,2,3,4,5,6 \}\) y
- \(B = \{2,4,6,8,10,12,14,16,18,20 \}\)
\[B-A =\{ 8,10,12,14,16,18,20 \}\]