Problema 1


Probabilidad y mi vida

Las decisiones forman parte de nuestras vidas, dia a dia tomamos decisiones que afectan nuestro futuro, para tomarlas en algunas ocasiones recurrimos a valorar el riesgo que podrían tener. ¿ En tu vida has tomado decisiones con información previa que te ha permitido valorar su riesgo?. o por el contrario tus decisiones han obedecido a corazonadas y sentimientos?. Esta pregunta solo es para reflexionar sobre el tema . No debes contestarla si no lo deseas.




Problema 2


Lanzamiento de un dado

Un experimento consiste en lanzar un dado y observar el número de puntos en su cara superior. Algunos eventos aleatorios que se pueden definir a partir de este experimento pueden ser:

  • A: sacar 2
  • B: sacar un número par
  • C: sacar un número mayor a 2
  • D: obtener A y B
  • E: obtener A o B o ambos
  • F: obtener A y C


  • Describa el espacio muestral asociado al experimento aleatorio
  • Liste cada uno de los eventos aleatorios A hasta F
  • Represéntelos mediante un diagrama de Ven
  • Determine en cada caso las probabilidades asociadas a cada evento aleatorio




Problema 3


Faltar a clases

En un grupo de 100 estudiantes 30 residen por fuera de la ciudad, de los cuales 10 presentan altos niveles de inasistencia a clases, mientras que 35 de los que residen dentro en la ciudad también presentan altos niveles de inasistencia a clases.

  • Construya una tabla de probabilidades con la información anterior.
  • Represente también la información mediante un diagrama de Venn.
  • Identifique dos eventos simples y dos eventos conjuntos En cada caso escriba en palabras la probabilidad y su resultado
  • ¿Se podría afirmar que residir en la ciudad y no tener altos niveles de inasistencia a clases son eventos independientes?




Problema 4


Sobre costos en la construcción

Una empresa de construcción local descubrió a través de una investigación que solo el 20% de todos los trabajos son terminados a tiempo, mientras que el 30% sufrían sobrecostos. Además, los sobrecostos se presentan en el 75% de las veces en la que los trabajos se terminaron a tiempo. Carlos, gerente de la empresa desea conocer que tan probable es que un proyecto no tenga sobrecostos y se termine a tiempo. Esto le permitirá tomar decisiones en caso de ser necesario. Ayude a Carlos a resolver su interrogante.




Problema 5


Muertes por accidentes de transito

Se sabe que los accidentes de tránsito en su mayoria ocurren durante la noche de los sábados y se deben en un 65% la ingesta excesiva de alcohol, un 25% se deben a la imprudencia del conductor y el resto a otras causas, (fallo mecánico…etc.). En estos accidentes, el resultado es nefasto en el 30% de las veces para el primer caso, un 20% en el segundo y el 5% en el tercero. Una empresa de salud que presta servicios de ambulancias quiere que Usted le ayude a pronosticar cuál es la causa del accidente más probable, sabiendo que este hecho ha tenido resultados nefastos. Con esta información la empresa pretende tomar decisiones sobre el equipamiento que deben tener sus vehículos, dando prioridad a los elementos relacionados con mayor probabilidad de ocurrencia. Ayude a la compañía de salud a establecer el orden de estas prioridades.




Problema 6


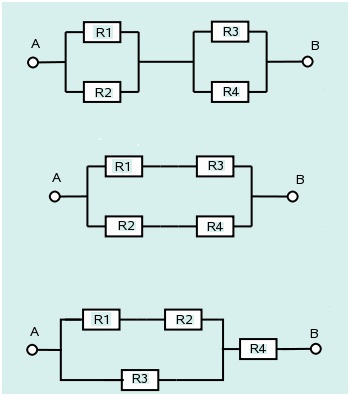
Sistema de seguridad:

Uno de los sistemas de seguridad de la universidad funciona mediante la conexión de cuatro componentes como se muestra en las figuras. Suponga que estos componentes funcionan de manera independientes y que la probabilidad de que falle cada uno de los componentes R1, R2, R3y R4 son respectivamente: \(0.10\), \(0.05\), \(0.10\) y \(0.20\). Con el fin de tener la mejor composición de ellos, es decir la mayor confiabilidad de funcionamiento, el director de recursos físicos le pide a determine cuál es la mejor configuración del sistema.




Problema 7


Delincuentes adictos a las drogas :

Un estudio sobre la conducta de un gran numero de delincuentes adictos a las drogas hace pensar que la probabilidad de una condena de dos años después del tratamiento podría depender del nivel de educación del delincuente. Las proporciones del numero total de casos que caen en cuatro categorías de educación y condena se muestran en la tabla siguiente:

Educación Condiciones dos años después del tratamiento
Condenado No condenado Totales
10 años o más 0.10 0.30 0.40
9 años o menos 0.27 0.33 0.60
Totales 0.37 0.63 1.00


Suponga que se selecciona un delincuente del programa de tratamiento y se esta interesado en los siguientes eventos :

\(A\): El delincuente tiene 10 años de educación o más

\(B\): El delincuente es condenado dos años después de completar el tratamiento


Encuentre las probabilidades para los eventos:

  • \(A\)
  • \(B\)
  • \(A \cap B\)
  • \(A \cup B\)
  • \(A'\)
  • \((A \cap B)'\)
  • \((A \cup B)'\)




Problema 8

Consejeria Académica


En una universidad de la región hay 4135 estudiantes distribuidos en tres grupos. Primeros semestre (1 a 3), mitad de carrera (4 a7) y final de carrera (8 a 10). Esta población esta conformada por estudiantes que realizan actividades extracuricolares y aquellos que no participan en ninguna actividad, distribuidos como se muestra en la siguiente tabla:

library(knitr)

x <- c(1250, 465, 270, 1530, 350, 270)
m <- matrix(x, nrow = 3)
colnames(m) <- c("MU", "MU*")
rownames(m) <- c("Primeros semestres", "Mitad de carrera", "Final de carrera")

kable(m, caption = "Tabla de Resultados por Etapa de la Carrera", align = "c")
Tabla de Resultados por Etapa de la Carrera
MU MU*
Primeros semestres 1250 1530
Mitad de carrera 465 350
Final de carrera 270 270
  • MU : Participa de actividades programadas por el Medio Universitario
  • MU* : No participa de actividades programadas por el Medio Universitario


Se ha encomendado a un grupo de profesores consejeros, seleccionar un estudiante de este grupo para guiarlos académicamente en su proceso de formación. El grupo de profesores está conformado por Sandra, Isabel, David, Daniel y Gerardo

Sandra prefiere que el grupo de estudiantes a su cargo sean estudiantes de primeros semestre y que participan en actividades del Medio Universitario (MU) . Isabel en cambio los eligirá dentro del grupo de estudiantes que está finalizando carrera, los que prefieren no participar en actividades del MU. Por su parte David desea estudiantes sean del rango intermedio o mitad de carrera, pues ellos no han realizado la escogencia del énfasis. Daniel solicita un listado de los estudiantes que participan e actividades del MU y de ellos desea que el estudiante a su cargo esté cursando últimos semestre. Finalmente Gerardo solo quiere que el estudiante seleccionado para su acompañamiento sea de primeros semestre. Si en cada caso los estudiantes son seleccionados de manera aleatoria de toda la población tiene la mayor probabilidad de ver cumplido sus deseos?