Unidad 4.2

Simulación

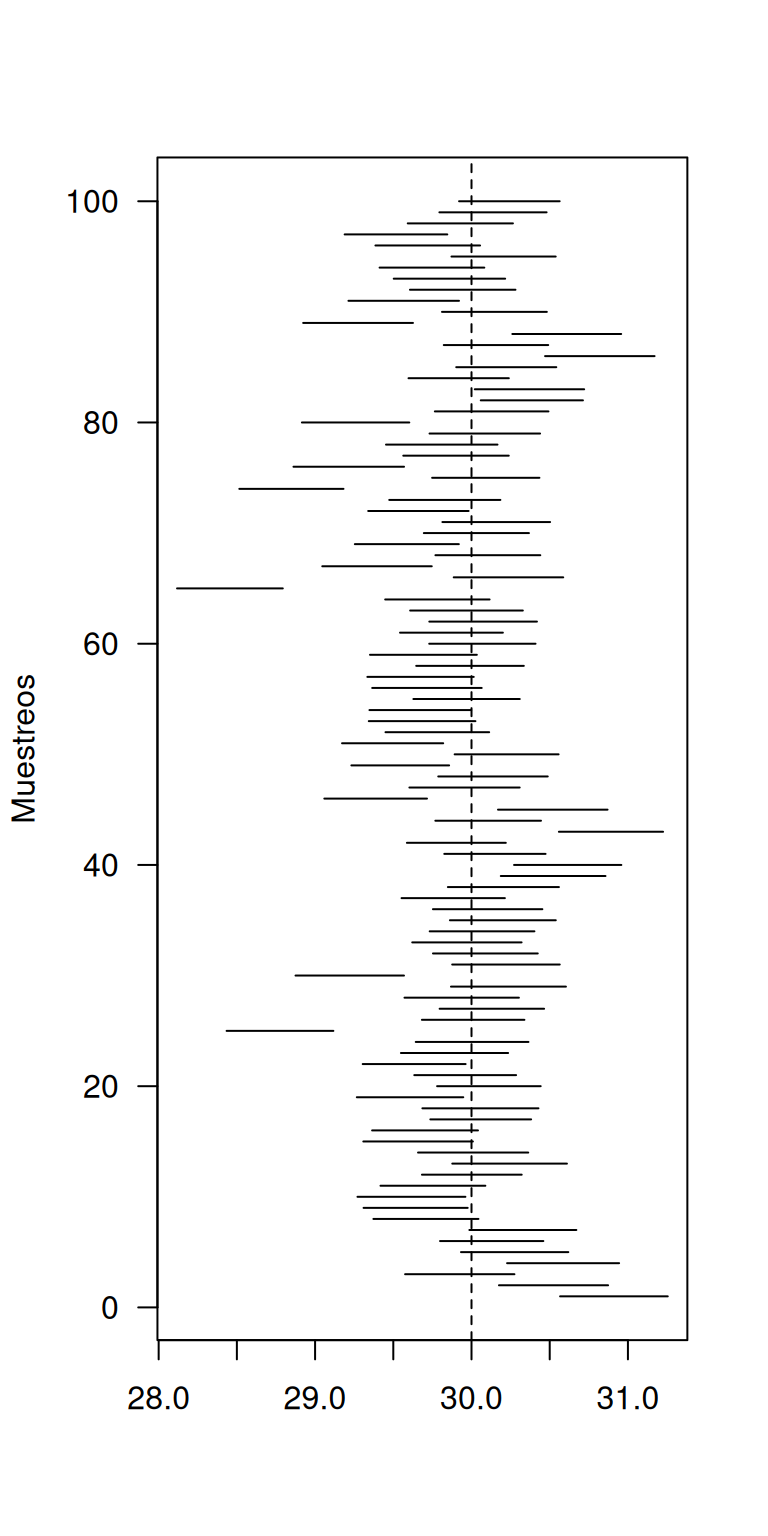
Con el fin de entender el concepto de confianza se propone la simulacion como estrategia. Inicialmente se genera de manera simulada un conjunto de 100 muestras (m=100) cada una de tamaño n=200, de una población con distribución normal con \(\mu=30\) y varianza \(\sigma^2=10\) y un valor de confianza del 95% (\(\alpha=0.05\))

La gráfica dibuja los 100 intervalos de confianza en el cual se pueden observar algunos unos pocos que no contienen el parametro (\(\mu=30\))

Confianza

m= 100 ## número de experimentos
n=300 ## tamaño de muestra
mux=30 # media poblacion 
sdx=sqrt(50)  # desviacion poblacion
a=0.05
x=rnorm(n*m, mux, sdx)
muestras=matrix(x, nrow = m)

icm=function(xx){
  mxx=mean(xx)
  sdxx=sd(xx)
  p=1-a/2
  lsxx=mxx+pnorm(p)*sdxx/sqrt(n)
  lixx=mxx-pnorm(p)*sdxx/sqrt(n)
  return(c(lixx,lsxx))
}

ICa=apply(muestras, 1,icm)

plot(1:100, type = "n",
     xlim = range(ICa),
     ylab = "Muestreos", 
     las=1, 
     xlab=" ")
abline(v = mux, lty = 2) ## la media poblacional.
for(i in 1:100) {
  segments(ICa[1,i], i, ICa[2,i], i)
}

Estimaciones

IC para una media

Intervalo de confianza para una media

Como ejemplo se estima un IC para la la nota final de los estudiantes que cursaron la asignatura de Matemáticas Fundamentales, para una muestra de n=180

t.test(muestra1$NF,conf.level = 0.95)$conf.int

IC para una proporción

Intervalo de confianza para una proporción

Como ejemplo se estima un intervalo de confianza para una muestra de tamaño 1000 para la proporción de fallecidos por covid en el Valle

ingciv=as.numeric(muestra1$CAR=="CIV")
t1=table(ingciv)
prop.test(t1[1],180, conf.level = 0.95)$conf.int

IC para una varianza

Para calcular el intervalo de confianza para una varianza, he creado la siguiente función, dado que no está disponible en R

# parametros de entrada : x variable 
#                         a alpha (confianza del 95% : a=0.05) 

ic.var=function(x,a){
  n=length(x)
    per.chi2=qchisq(c(1-a/2, a/2), n-1)   # percentiles chi-cuadrado para 95% de confianza
  icvar=(n-1)*var(x)/per.chi2
  return(icvar)
}
x1=rnorm(100)
ic.var(x1, 0.05)

IC comparación varianzas

Intervalo de confianza para la comparación de varianzas

Como ejemplo se toman dos muestras de las edades para las personas contagiadas por covid en el Valle

nota.civ=c(3,1.5,1,4.7,1.7,3.1,3,2.6,3.4,3.3,4.7,2.3,3.7,1.1,2.4,3.6,3.1,0.9,1.2,0.8,3.1,2.5,2.2,3.2,2,2.2,2,3.6,2.5,2.3,3.1,2.2,4,3,3.6,2.4,4.1,3.7,3,2.4,3,3.8,2.1,3,3.9,2,4.1,1.7,3,4.1,1.4,3.2,4.4,3.2,3.8,2.2,2.3,4.5,4.5,2.5,3.6,4.4,1.7,1.7)
nota.ind=c(3.5,3.3,2.4,4.6,3.8,2.5,3.1,3.5,4.7,1.2,3.2,0.7,0.8,3.4,4.1,1.5,3.2,4.2,3.7,1.3,3.2,4.7,3,4.6,2.4,4.5,4.4,4.3,3.9,4.3,3.1,1.8,3.1,4.3,3.1,2.6,3.1,4.1,4.3,3.5,3.3,3.7,3.6,2.4,3.5,4.3,3.3,2.2,3.5,4.5,4.1,0.9,3,2,3.8,2.1,2)

var.test(nota.civ, nota.ind)$conf.int 

[1] 0.5374026 1.5023015
attr(,"conf.level")
[1] 0.95

IC medias grupos independientes

Intervalo de confianza para la comparación de medias grupos independientes, suponiendo varianzas iguales

Como ejemplo se toman dos muestras para comparar la edad de las personas contagiadas por covid en dos grupos independientes

t.test(nota.civ, nota.ind,
       mu = 0, 
       paired = FALSE, 
       var.equal = TRUE,
       conf.level = 0.95 )$conf.int 

Intervalo de confianza para la comparación de medias grupos independientes, con varianza diferentes

En este caso se toman dos muestras de grupos independientes, solo se realiza el procedimiento para mostrar la sintaxis en el caso de que las varianza sean diferentes

 t.test(nota.civ, nota.ind,
       mu = 0, 
       paired = FALSE, 
       var.equal = FALSE,
       conf.level = 0.95 )$conf.int

IC comparación proporciones

Comparación de proporciones

Para el ejemplo se toma una muestra de tamaño 1000 y se compara las proporciones de personas contagiadas y con estado grave y con estado moderado

nciv=65
nind=58
prop.test(c(nciv,nind),c(180,180), conf.level = 0.95)$conf.int