Unidad 3.3
dgonzalez

Actividad 332
Cada estudiante deberá seleccionar un problema dentro de los primeros tres enunciados presentados a continuación. Además del problema seleccionado deberá también realizar el problema 4. En total debe presentar dos problemas.
Problemas de simulación
Alejandra es la persona encargada de las compras para un gran laboratorio de investigaciones biológicas. Uno de los principales insumos utilizados en el laboratorio son reactivos especializados, los cuales se compran a dos fabricantes internacionales de gran renombre. Debido a problemas logísticos durante el transporte, se estima que cada unidad de reactivo tiene una probabilidad de \(0.03\) de estar contaminada o defectuosa en el caso del primer fabricante, y una probabilidad de \(0.05\) para el segundo fabricante. Usted recibe un envío de \(100\) reactivos.
- Sea \(X\) el número de unidades defectuosas en el envío del fabricante 1 y \(Y\) del número de unidades defectuosas provenientes del fabricante 2 . ¿Cuáles son las distribuciones de las variables \(X\) y \(Y\)?
- Genere muestras simuladas de tamaño \(1000\) a partir de las distribuciones de \(X\) y \(Y\).
- Utilice las muestras para estimar la probabilidad de que el número total de unidades defectuosas sea menor a diez.
- Utilice las muestras para estimar la probabilidad de que el envío del primer fabricante se presentaran más unidades defectuosas que el envío realizado por el segundo fabricante.
- Construya una gráfica de probabilidad normal para el número total de unidades defectuosas. ¿Sigue una distribución normal?
La edad de una antigua pieza de materia orgánica se puede estimar a partir de la tasa a la que emite partículas beta como resultado del decaimiento del carbono-14. Por ejemplo , si X es el número de partículas emitidas durante diez minutos por un fragmento óseo con 10000 años de antigüedad que contiene 1 g de carbono, entonces X tiene una distribución de Poisson con media \(\lambda=45.62\) . Un arqueólogo descubrió un pequeño fragmento óseo que contiene 1 g de carbono. Si t es la edad desconocida del hueso, en años, el arqueólogo contar{a el número X de partículas emitidas en diez minutos y calculará una edad estimada \(\widehat{t}\) con la fórmula:
\[\widehat{t}=\dfrac{\ln 15.3 - \ln (X/10)}{0.0001210} \]
El arqueólogo no lo sabe, pero el hueso tiene exactamente \(10000\) años de antigüedad, por lo que \(X\) tiene una distribución de Poisson con \(\lambda=45.62\).

- Genere una muestra simulada de 10000 valores de \(X\) y sus correspondientes valores de \(\widehat{t}\).
- Estime la media de \(\widehat{t}\).
- Estime la desviación estándar de \(\widehat{t}\).
- Estime la probabilidad de que \(\widehat{t}\) esté a 1000 años con una edad real de 10000 años.
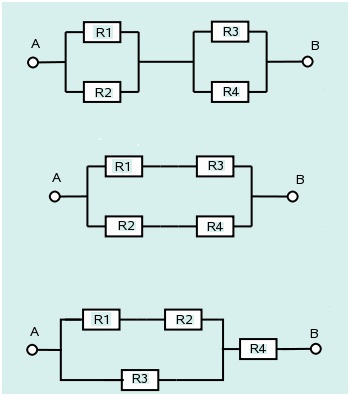
Tres sistemas están compuestos por los componentes
R1,R2, R3 y R4
conectados, como lo muestra las siguientes figuras. El tiempo de vida en
meses de los componentes R1 y R3 sigue una
distribución lognormal con \(\mu=2\) y
\(\sigma=1\) y la distribución en meses
de los componentes R2 y R4 una distribución
lognormal con \(\mu=1\) y \(\sigma=0.1\). El sistema solo funciona si
A y B lo hacen.
- Genere por simulación un gran número (al menos \(1000\)) de los tiempos de vida de los sistemas
- Estime la media del tiempo de vida para cada sistema.
- Estime la probabilidad de que los sistemas fallen en un tiempo inferior a dos meses.
- Estime el \(20^{o}\) percentil (\(P_{20}\)) de los tiempos de vida del primer sistema .
- Construya una gráfica de probabilidad normal de los tiempo de vida para cada sistema. ¿Los tiempos de vida de los sistemas tienen una distribución aproximadamente normal?
- Construya un histograma de los tiempos de vida de los sistemas. ¿Están sesgados a la izquierda, sesgados a la derecha, o son aproximadamente simétricos?
Estimación del valor de \(\pi\) . LA siguiente figura sugiere como estimar el valor de \(\pi\) con una simulación. En la figura, un círculo con área igual a \(\pi/4\), está inscrito en un cuadrado cuya área es igual a 1. Se elige de forma aleatoria 100 puntos dentro del cuadrado . La probabilidad de que un punto esté dentro del círculo es igual a la fracción del área del cuadrado que abarca a este, la cual es \(\pi/4\). Por tanto, se puede estimar el valor de \(\pi/4\) al contar el número de puntos dentro del círculo, que es 79 para obtener la estimación de \(\pi/4 \approx 0.76\) . De este último resultado se concluye que \(\pi \approx 4(0.79) =3.14\) . Este ejercicio presenta un experimento de simulación que fue diseñado para estimar el valor de \(\pi\) al generar 1000 puntos en el cuadrado.
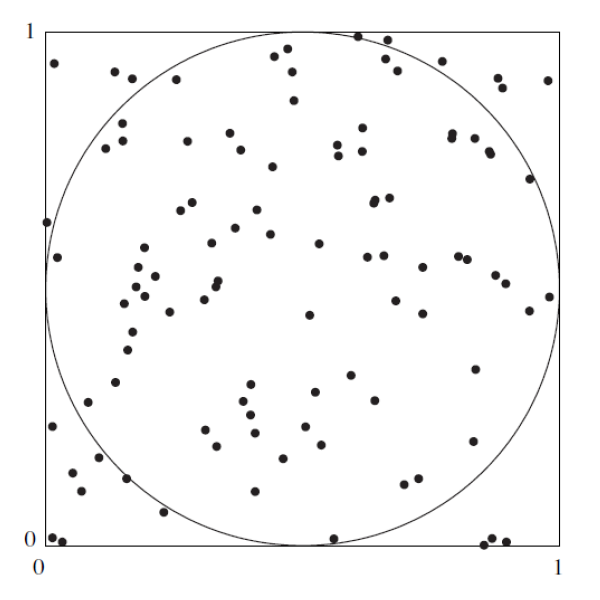
Genere 1000 coordenadas \(x\): \(X_{1}\), . . . , \(X_{1000}\). Utilice la distribución uniforme con valor mínimo de \(0\) y valor máximo de \(1\). La distribución uniforme genera variables aleatorias que tienen la misma probabilidad de venir de cualquier parte del intervalo \((0, 1)\).
Genere \(1000\) coordenadas \(y\) : \(Y_{1}, . . . , Y_{1000}\), utilizando nuevamente la distribución uniforme con valor mínimo de \(0\) y valor máximo de \(1\).
Cada punto \((X_{i},Y_{i})\) se encuentra dentro del círculo si su distancia desde el centro \((0.5, 0.5)\) es menor a \(0.5\). Para cada par \((X_{i},Y_{i})\) determine si la distancia desde el centro es menor a \(0.5\). Esto último se puede realizar al calcular el valor \((X_{i}-0.5)^{2}+(Y_{i}-0.5)^{2}\), que es el cuadrado de la distancia, y al determinar si es menor que \(0.25\).
¿Cuántos de los puntos están dentro del círculo? ¿Cuál es su estimación de \(\pi\)? (Nota: Con sólo 1000 puntos, es probable que su estimación sea inferior por 0.05 o más. Una simulación con 10000 y 100000 puntos tiene mayores probabilidades de dar como resultado una estimación muy cercana al valor verdadero
Ejercicios tomados de Navidi(2006)